|
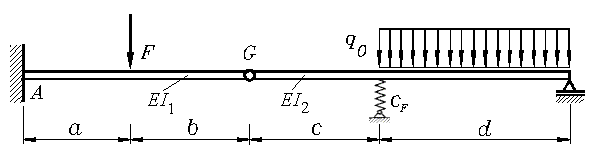
% Differenzenverfahren: Gerader Träger mit Gelenk und Feder (Aufgabe 18-10)
clear all
La = 220 ;
Lb = 260 ;
Lc = 300 ;
Ld = 420 ;
EI1 = 2.1e5*2400 ;
EI2 = 2.1e5*800 ;
cF = 300 ;
q0 = 2 ;
F = 800 ;
L = La+Lb+Lc+Ld ; % Länge
EIB = EI1 ; % Bezugs-Biegesteifigkeit
nA = 480 ; % Anzahl der Abschnitte
n = nA + 5 ; % Anzahl der Gleichungen
h = L / nA ; % Schrittweite
A = zeros (n,n) ; % Matrix A
b = zeros (n,1) ; % Rechte Seite b
qi = zeros (n,1) ; % Linienlast
mi = zeros (n,1) ; % Ii = mi * IB
ki = zeros (n,1) ; % Bettungszahlen an Stuetzpunkten
% Markante Punkte:
iKraft = round (nA * La/L + 3) ;
iGelenk = round (nA * (La+Lb)/L + 3) ;
iFeder = round (nA * (La+Lb+Lc)/L + 3) ;
iRechts = n - 2 ;
% Belastung
qi(iFeder:iRechts) = q0 ;
qi(iKraft) = F/h ;
% Biegesteifigkeit (mue-Werte):
mi(1:iGelenk-1) = EI1/EIB ;
mi(iGelenk) = 0 ;
mi(iGelenk+1:n) = EI2/EIB ;
% Feder:
ki(iFeder) = cF/h ;
%Randbedingungen:
A(1:2,1:5) = [0 0 1 0 0 ; ...
0 -1 0 1 0] ; % Einspannung links
A(n-1:n,n-4:n) = [0 mi(iRechts) -2*mi(iRechts) mi(iRechts) 0 ; ...
0 0 1 0 0] ; % Loslager rechts
for i=3:n-2 % Matrix A:
A(i,i-2:i+2)=[mi(i-1) -2*(mi(i-1)+mi(i)) mi(i-1)+4*mi(i)+mi(i+1)+ki(i)*h^4/EIB ...
-2*(mi(i)+mi(i+1)) mi(i+1)] ;
end
% Rechte Seite b:
for i=3:iRechts
b(i) = qi(i)*h^4/(EIB) ;
end
v = A \ b ; % Lösung des Gleichungssystems (Berechnung der Durchbiegung v)
clf;
z = 0 : h : L ;
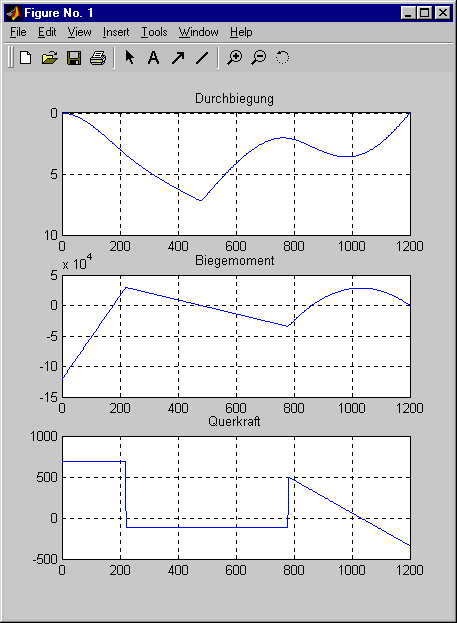
subplot (3,1,1) ; plot (z , v(3:n-2)) , axis ij , grid on , title
('Durchbiegung') % Biegelinie
for i=3:n-2
Mb(i) = -mi(i)*EIB * (v(i-1)-2*v(i)+v(i+1))/h^2 ; % Biegemoment
FQ(i) = 0.5*EIB * (mi(i-1)*v(i-2)-2*mi(i-1)*v(i-1)+(mi(i-1) ...
-mi(i+1))*v(i)+2*mi(i+1)*v(i+1)-mi(i+1)*v(i+2))/h^3 ; % Querkraft
end
subplot (3,1,2) ; plot (z , Mb(3:n-2)) , grid on , title
('Biegemoment') % Momentenverlauf
subplot (3,1,3) ; plot (z , FQ(3:n-2)) , grid on , title ('Querkraft') % Querkraftverlauf
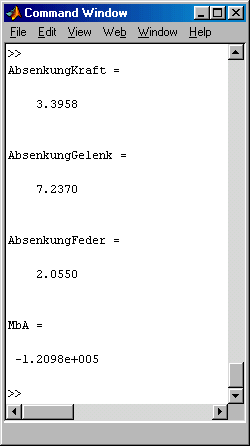
AbsenkungKraft = v(iKraft) % Ausgabe in das Command window:
AbsenkungGelenk = v(iGelenk) % Zahlenwerte der Verschiebungen ...
AbsenkungFeder = v(iFeder) % ... an drei speziellen Punkten ...
MbA = Mb(3) % ... und das Einspannmoment am Punkt A
|