Zur Startseite

Lösung mit MATLAB

Der skizzierte Knickstab mit konstanter Biegesteifigkeit ist am linken Rand starr eingespannt und am rechten Rand durch eine Feder gefesselt.

Gegeben:
E = 210000 N/mm² ; I = 50 mm⁴ ;
l = 0,5 m ;  c = 2 N/mm .

1. Mit dem RITZschen Verfahren ist mit einem fünfgliedrigen Ansatz mit Potenzfunktionen die Knickkraft F_kr näherungsweise zu berechnen. Die Berechnung ist mit folgenden Testrechnungen zu verifizieren:
    
2. Die Federsteifigkeit ist gleich Null zu setzen, das so ermittelte Ergebnis ist mit dem Euler-Fall “Einseitig starr eingespannt, am Kraftangriffspunkt frei” zu vergleichen.
    
3. Für die Federsteifigkeit c ist ein sehr großer Wert anzunehmen. Das Ergebnis ist mit dem 3. Euler-Fall zu vergleichen.
    
4. Zusätzlich zur Lagerung nach Variante c ist noch eine sehr steife Drehfeder am Kraftangriffspunkt anzubringen. Das Ergebnis ist mit dem 4. Euler-Fall zu vergleichen.

Das Problem wird mit dem Verfahren von RITZ auf der Basis des hier beschriebenen Algorithmus gelöst. Die Ansatzfunktionen müssen die beiden geometrischen Randbedingungen am linken Rand (Verschiebung und Ableitung der Verschiebung gleich Null) erfüllen, so dass z²,  z³, z⁴ usw. als Vergleichsfunktionen zulässig sind. Wegen der numerischen Stabilität der Rechnung wird auch hier dringend empfohlen, die Koordinaten (mit der Länge des Stabes) zu normieren. Deshalb werden folgende Ansatzfunktionen verwendet:

v₁ = z²/l²   ;   v₂ = z³/l³   ;   v₃ = z⁴/l⁴   ;   v₄ = z⁵/l⁵   ;   v₅ = z⁶/l⁶   .

Die nachfolgend gelistete M-Datei ist so geschrieben, dass sie für andere Knickstab-Probleme leicht modifizierbar ist, wobei nur die farblich und durch Kommentare gekennzeichneten drei Bereiche modifiziert werden müssen:

1. Nach der Definition der Parameter der Aufgabenstellung werden die Ansatzfunktionen (hier die 5 oben genannten einfachen Funktionen) definiert. Das Script ist für maximal 5 Ansatzfunktionen ausgelegt. Wenn es mit weniger als 5 Ansatzfunktionen genutzt werden soll, muss man nur den Wert für m entsprechend ändern. Dann werden nur die ersten Polynome genutzt (bei m = 3 werden also P4 und P5 im weiteren Verlauf des Scripts nicht berücksichtigt). Die restlichen Polynome sollten aber nicht gelöscht werden, weil man sonst alle späteren Zeilen, die darauf Bezug nehmen, auch ändern müsste.
    
2. Die Integrale werden numerisch gelöst (Simpsonsche Regel). Die Anzahl der Abschnitte, in die die Trägerlänge unterteilt wird, ist mit n = 100 festgelegt, was wohl in der Regel mehr als ausreichend ist (kann jedoch bei Bedarf auf einen beliebigen geradzahligen Wert geändert werden).
   
   Für die nS = n + 1 Stützstellen müssen die Werte für die Biegesteifigkeit (hier konstant für alle Punkte) und die auf die kritische Last (Eigenwert) bezogene Normalkraft “F_N-Quer” bereitgestellt werden (wenn die Normalkraft - wie hier und bei den weitaus meisten praktischen Problemen - konstant mit dem Wert F_N = -F ist, gilt für alle Punkte F_N-Quer = 1).
   
   In diesem Bereich sollten auch die Punktnummern für die Punkte festgelegt werden, an denen Federn angreifen.
    
3. Bis auf die Berücksichtigung von Federn kann der gesamte restliche Algorithmus unverändert auch für andere Aufgaben übernommen werden: Die Berechnung der Funktionswerte und der ersten und zweiten Ableitungen an den Stützstellen wird von den Matlab-Funktionen polyval und polyder unterstützt, die numerische Integration wird in einer for-Schleife erledigt. Nach der numerischen Integration sind lediglich die Anteile von Federn zu ergänzen (vorbereitet sind die Zeilen für eine Feder und eine Drehfeder, können bei mehreren Federn entsprechend ergänzt werden). Danach ist der Aufbau der beiden Matrizen, die das allgemeine symmetrische Eigenwertproblem definieren, komplett.

% Ritzsches Verfahren für die Stabknickung: Aufgabe 33.13

clear all

% 11111111111 ANPASSEN AN DAS AKTUELLE PROBLEM VON HIER ... 111111111111111111111111111
% Parameter:
tl = 500   ;        
E  = 2.1e5 ;        
I  = 50    ;
c  = 2     ;

% Ansatzfunktionen und deren 1. und 2. Ableitungen:
m  = 5 ;                     % Anzahl der Ansatzfuntionen (wenn m < 5 gesetzt ...
P1 = [1/tl^2 0 0] ;          % ... wird, werden nur die ersten ...
P2 = [1/tl^3 0 0 0] ;        % ... m Ansatzfunktionen verwendet)
P3 = [1/tl^4 0 0 0 0] ;
P4 = [1/tl^5 0 0 0 0 0] ;
P5 = [1/tl^6 0 0 0 0 0 0] ;
% 11111111111 ... BIS HIER 111111111111111111111111111111111111111111111111111111111111

P1D = polyder (P1);
P2D = polyder (P2);
P3D = polyder (P3);
P4D = polyder (P4);
P5D = polyder (P5);

P1DD = polyder (P1D) ;
P2DD = polyder (P2D) ;
P3DD = polyder (P3D) ;
P4DD = polyder (P4D) ;
P5DD = polyder (P5D) ;

% ------------------------------------------------------------------------------------
% Vorbereitung der numerischen Integration und der Ergebnisauswertung:
n  = 100 ;               % Anzahl der Abschnitte für numerische Integration
dz = tl / n ;            % Breite eines Integrationsintervalls
nS = n + 1 ;             % Anzahl der Stützstellen
zS = 0 : dz : tl ;       % Koordinaten der Stützpunkte

EIS = zeros (nS , 1) ;
FNQ = zeros (nS , 1) ;

% 22222222222222 ANPASSEN AN DAS AKTUELLE PROBLEM VON HIER ... 222222222222222222222222
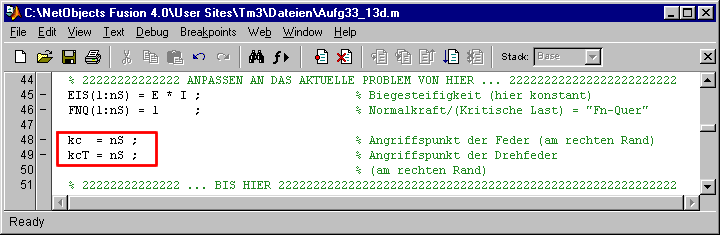
EIS(1:nS) = E * I ;                      % Biegesteifigkeit (hier konstant)
FNQ(1:nS) = 1    ;                      % Normalkraft/(Kritische Last) = "FN-Quer"

kc = nS ;                               % Angriffspunkt der Feder (am rechten Rand)
% kcT = round (n*tl1/tl + 1.1) ;         % Angriffspunkt einer Drehfeder im Abstand tl1
                                         % vom linken Rand
% 22222222222222 ... BIS HIER 222222222222222222222222222222222222222222222222222222222

% Funktionswerte und 1. und 2. Ableitung der Ansatzfunktionen an den Stützstellen
vS (:,1) = polyval (P1  , zS)' ;
vS (:,2) = polyval (P2  , zS)' ;
vS (:,3) = polyval (P3  , zS)' ;
vS (:,4) = polyval (P4  , zS)' ;
vS (:,5) = polyval (P5  , zS)' ;
vdS (:,1) = polyval (P1D , zS)' ;
vdS (:,2) = polyval (P2D , zS)' ;
vdS (:,3) = polyval (P3D , zS)' ;
vdS (:,4) = polyval (P4D , zS)' ;
vdS (:,5) = polyval (P5D , zS)' ;
vddS(:,1) = polyval (P1DD , zS)' ;
vddS(:,2) = polyval (P2DD , zS)' ;
vddS(:,3) = polyval (P3DD , zS)' ;
vddS(:,4) = polyval (P4DD , zS)' ;
vddS(:,5) = polyval (P5DD , zS)' ;

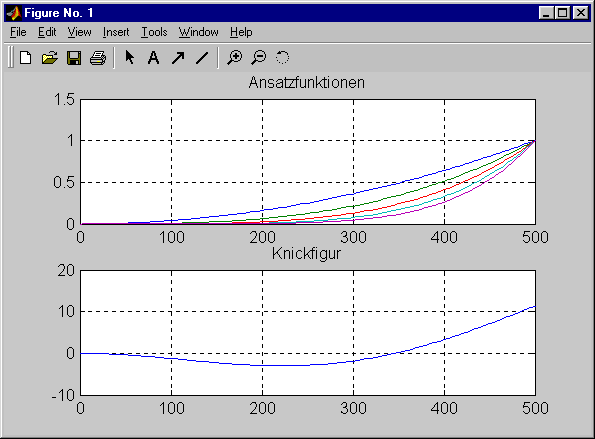
subplot(211) ; plot(zS , vS(:,1:m)) ; grid ; title('Ansatzfunktionen') ;

% ------------------------------------------------------------------------------------
% Aufbau des allgemeinen Matrizen-Eigenwertproblems:
K = zeros (m , m) ;
B = zeros (m , m) ;

for ii = 1:m                                         % Schleife über alle Gleichungen
  for jj = 1:m                                       % ii-te Zeile (Koeffizienten kij)
   Summe1 = EIS(1)*vddS(1,ii)*vddS(1,jj) + EIS(nS)*vddS(nS,ii)*vddS(nS,jj) ;
   Summe2 = FNQ(1)*vdS (1,ii)*vdS (1,jj) + FNQ(nS)*vdS (nS,ii)*vdS (nS,jj) ;
   faktor = 4 ;                                     % Numerische Integration ...
   for k = 2:n                                      % ... nach Simpsonscher Regel ...
     Summe1 = Summe1 + EIS(k) * vddS(k,ii) * vddS (k,jj) * faktor ;
     Summe2 = Summe2 +          vdS (k,ii) * vdS  (k,jj) * faktor ;
     if   (faktor == 4) faktor = 2 ;               
     else               faktor = 4 ;               
     end ;
   end
% 33333333333333 ANPASSEN AN DAS AKTUELLE PROBLEM VON HIER ... 3333333333333333333333333
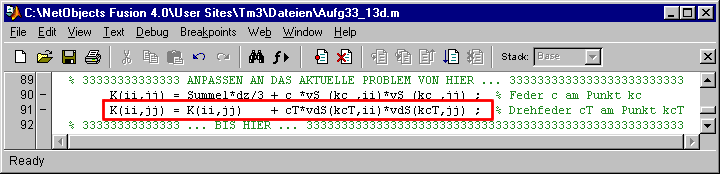
     K(ii,jj) = Summe1*dz/3 + c *vS (kc ,ii)*vS (kc ,jj) ; % Feder c am Punkt kc
   % K(ii,jj) = K(ii,jj)    + cT*vdS(kcT,ii)*vdS(kcT,jj) ;  % Drehfeder cT am Punkt kcT
% 33333333333333 ... BIS HIER ... 333333333333333333333333333333333333333333333333333333
   B(ii,jj) = Summe2*dz/3 ;
  end 
end

% Lösen des allgemeinen Eigenwertproblems:
[V D] = eig (K , B) ;
for i=1:m
   lambda(i) = D(i,i) ;                      % Eigenwerte
end
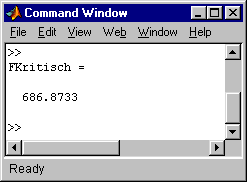
[Fkr , index] = min(lambda) ;                % Kleinster Eigenwert = Kritische Last
FKritisch = Fkr

vSchlange = vS(:,1:m) * V(1:m,index) ;       % Knickfigur zum kleinsten Eigenwert
subplot(212) ; plot(zS , vSchlange) ; grid ; title('Knickfigur') ;

Das durch die Matrizen K und B definierte allgemeine Eigenwertproblem wird von der Matlab-Function eig gelöst. Abgeliefert werden eine quadratische Matrix V, die spaltenweise die Eigenvektoren enthält (in einer Spalte stehen also die a_i-Werte des RITZ-Ansatzes, die zu einem Eigenwert gehören) und eine Diagonalmatrix D mit den Eigenwerten. Der kleinste Eigenwert ist identisch mit der kritischen Kraft F_kr, die in das Command Window ausgegeben wird.

In einem Graphik-Fenster werden einerseits sämtliche Ansatzfunktionen gezeichnet, so dass man eine optische Kontrolle hat, ob die geometrischen Randbedingungen von allen Funktionen erfüllt werden, andererseits wird die aus den a_i-Werten des zur kritischen Last gehörenden Eigenvektors und den Ansatzfunktionen die Knickfigur berechnet und graphisch dargestellt.

Für die Aufgabenstellung a (realisiert in dem oben gelisteten Script) erhält man folgende Ergebnisse:

www.DankertDankert.de