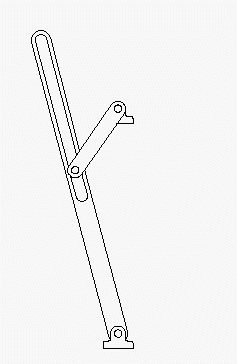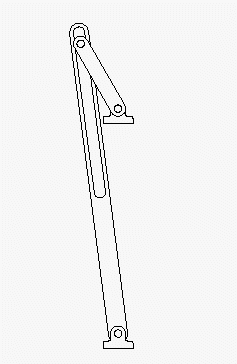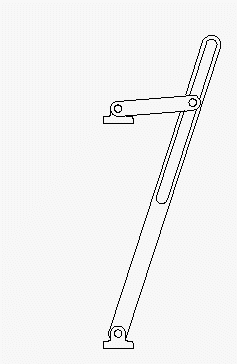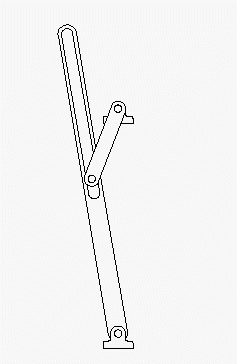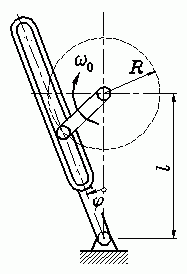
Im Kapitel "Kinematik starrer Körper" wird die nebenstehend skizzierte Aufgabe behandelt: Eine Kurbel mit dem Radius R läuft mit der konstanten Winkelgeschwindigkeit ω0 um und nimmt dabei eine Schwinge mit. Es sollen das Bewegungsgesetz der Schwinge φ(t), ihre Winkelgeschwindigkeit ωS(t) und Winkelbeschleunigung αS(t) als kinematische Diagramme dargestellt werden.
Es wird das Abmessungsverhältnis β = l/R = 3 angenommen. Als Beginn der Zeitzählung t = 0 wird die vertikale Lage der Schwinge φ = 0 gewählt, bei der der Mitnehmer der Kurbel seine tiefste Lage hat. Mit relativ einfachen geometrischen Überlegungen kann φ(t) aufgeschrieben werden, ωS(t) und αS(t) ergeben sich dann als erste bzw. zweite Ableitung von φ(t) nach der Zeit:
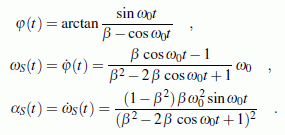
Die nachfolgend zu sehenden Animationen links bzw. rechts geben eine Vorstellung von der Bewegung (wurden mit dem Programm SolidWorks erstellt, sind auch mit Klick auf ein Bild als AVI-Dateien verfügbar).
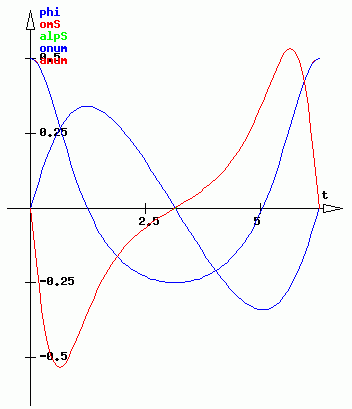
Für die Erzeugung der Bewegungsgesetze (nachfolgende Grafik in der Mitte) wurde das unter TM-interaktiv verfügbare Programm "Funktionen analysieren" benutzt. Dieses Programm gestattet auch das numerische Differenzieren von Funktionen, das hier zur Kontrolle der gebildeten Ableitungen genutzt wurde. Dargestellt sind (für einen kompletten Umlauf der Kurbel) die drei oben angegebenen Funktionen und zusätzlich die erste und zweite Ableitung der Funktion φ(t). Zu sehen sind trotzdem nur drei Kurven, weil sich die beiden Winkelgeschwindigkeits-Funktionen und die beiden Winkelbeschleunigungs-Funktionen total überdecken (wie es natürlich sein muss). Die ausführlich beschriebene Bedienung des Programms zur Erzeugung dieser Grafik findet findet man auf der Seite "Funktionen analysieren" als Beispiel 2.