Aufgabe

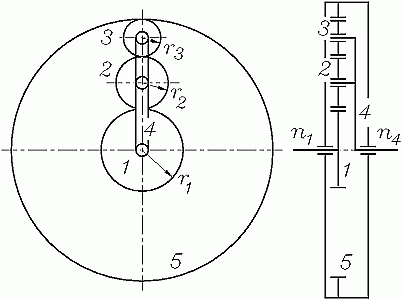
Bei dem skizzierten Planetengetriebe treibt der Steg 4 die beiden Planetenräder 2 und 3, die mit dem Sonnenrad 1 bzw. dem Gehäuse 5 im Eingriff sind.

Gegeben: r₁, r₂, r₃.

1. Man ermittle das Drehzahlverhältnis n₁/n₄ unter der Annahme, dass das Gehäuse 5 festgehalten wird.
2. Welche Drehzahl n₁ hat das Sonnenrad, wenn der Steg mit n₄ und das Gehäuse (gleichsinnig) mit n₅ gedreht werden?

Lösung

Es wird nur die Aufgabenstellung b behandelt, weil Aufgabenstellung a als Sonderfall mit n₅=0 in der Lösung enthalten ist

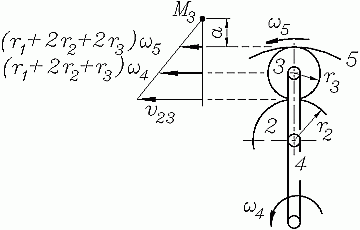
Die nebenstehende Skizze zeigt die Geschwindigkeiten für drei Punkte des Planetenrades 3: Der Mittelpunkt wird vom Steg 4 mit der Winkelgeschwindigkeit ω₄ auf seiner Kreisbahn mit dem Radius (r₁+2r₂+r₃) mit der Bahngeschwindigkeit (r₁+2r₂+r₃)ω₄ bewegt, der obere mit dem Gehäuse im Eingriff stehende Punkt dementsprechend mit (r₁+2r₂+2r₃)ω₅. Im Kapitel "Kinematik starrer Körper" wird gezeigt, wie man aus der Kenntnis zweier paralleler Geschwindigkeiten die Lage des Momentanpols M₃ mit Hilfe der Strahlensatzfigur bestimmen kann, um dann die Geschwindigkeiten aller anderen Punkte des starren Körpers (hier zum Beispiel die Geschwindigkeit v₂₃) berechnen zu können.

Die Skizze zeigt, dass es hier noch etwas einfacher geht, denn die Geschwindigkeit des Mittelpunkts muss der Mittelwert der beiden Geschwindigkeiten am oberen bzw. unteren Punkt des Rades 3 sein. Aus

errechnet man:

Weil die beiden Planetenräder miteinander im Eingriff sind, ist v₂₃ auch die Umfangsgeschwindigkeit am oberen Punkt des Rades 2, und mit dessen Mittelpunktsgeschwindigkeit (r₁+r₂)ω₄ (infolge der Zwangsführung durch den Steg) kann für das Rad 2 die gleiche Rechnung ausgeführt werden wie für Rad 3, und man kommt zur gemeinsamen Umfangsgeschwindigkeit v₁₂ von Planetenrad 2 und Sonnenrad 1. Daraus kann nach ω₁=v₁₂/r₁ die Winkelgeschwindigkeit des Sonnenrades berechnet werden. Weil alle Winkelgeschwindigkeiten mit den Drehzahlen über ω=2πn verknüpft sind, können die Winkelgeschwindigkeiten durch die Drehzahlen ersetzt werden. Der gemeinsame Faktor 2π kürzt sich heraus, und man erhält das Ergebnis:

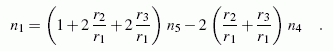
Für den Sonderfall n₅=0 (feststehendes Gehäuse) liest man daraus ab:

Das Minuszeichen zeigt an, dass bei feststehendem Gehäuse der Steg und das Sonnenrad entgegengesetzte Drehrichtungen haben.

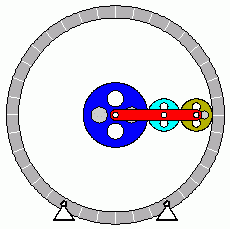
Animation der Bewegung

Planetengetriebe mit starrem Gehäuse

Nebenstehend sind die beiden Varianten dargestellt. Dafür wurden die Abmessungsverhältnisse r1/r2=2 und r2/r3=1 gewählt. In beiden Bildern rotiert der (rote) Steg mit der konstanten Drehzahl n4. Im linken Bild ist das Gehäuse feststehend, im rechten Bild rotiert es mit n5=−n4/2 (halbe Drehzahl mit entgegengesetzter Drehrichtung). Die oben angegebenen Formeln werden bestätigt: Beim feststehenden Gehäuse rotiert das (blaue) Sonnenrad bei diesen Abmessungen mit der doppelten Drehzahl des Steges (und entgegengesetzter Drehrichtung). Bei den Abmessungsverhältnissen und den angenommenen Antriebsdrehzahlen für das rotierende Gehäuse (rechtes Bild) erhält man nach diesen Formeln für das Sonnenrad n1=−3,5n4, was ebenfalls durch die Animation bestätigt wird.

Planetengetriebe mit drehendem Gehäuse