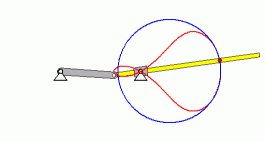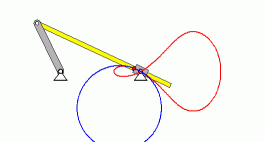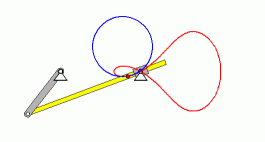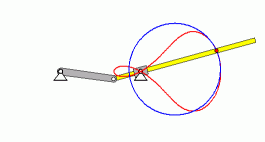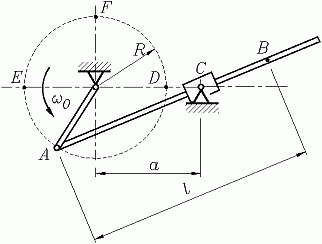
Im Kapitel "Kinematik starrer Körper" wird die nebenstehend skizzierte Aufgabe formuliert:
Eine Kurbel dreht sich mit der konstanten Winkelgeschwindigkeit ω0 und nimmt die Stange A-B mit. Bei t = 0 befindet sich A im Punkt D.
Gegeben: R ; ω0 ; a/R = 1,5 ; l/R = 2 .
Unter Verwendung eines Koordinatensystems mit Ursprung im Punkt C ermittle man
- die Bahnkurve von B in Parameterdarstellung x(t) und y(t),
- die Komponenten vBx und vBy des Geschwindigkeitsvektors des Punktes B allgemein,
- die Beträge der Geschwindigkeiten des Punktes B, wenn A sich in E bzw. F befindet.
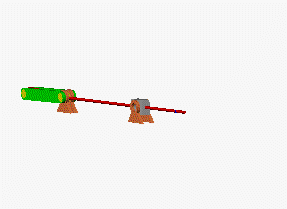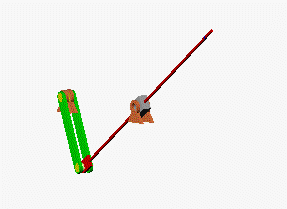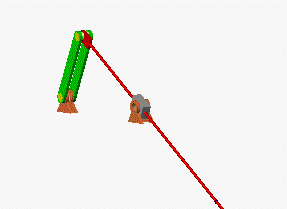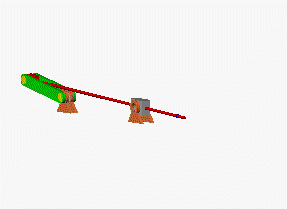
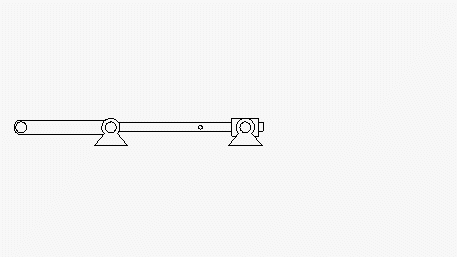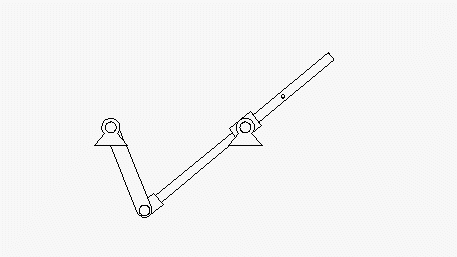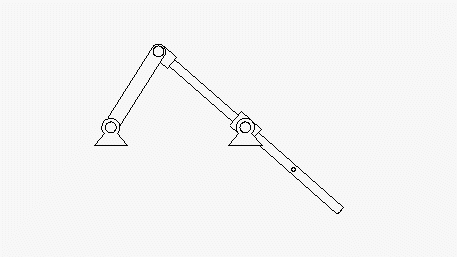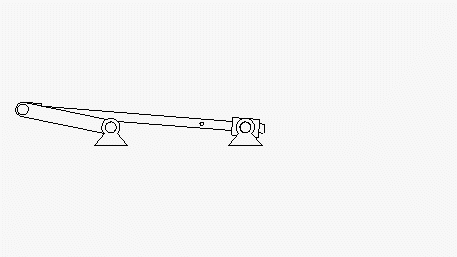 Zunächst sollen die nebenstehend zu sehenden
Animationen eine Vorstellung
von der Bewegung geben (wurden mit dem Programm SolidWorks erstellt,
sind auch mit Klick auf ein Bild als AVI-Dateien verfügbar).
Zunächst sollen die nebenstehend zu sehenden
Animationen eine Vorstellung
von der Bewegung geben (wurden mit dem Programm SolidWorks erstellt,
sind auch mit Klick auf ein Bild als AVI-Dateien verfügbar).
Außerdem wird auf die Seite "Krümmungsradius und Krümmungskreis" verwiesen, die zwar ein anderes Thema behandelt, aber für die hier betrachtete Kurbelschleife eine Animation zeigt, die die Entstehung der Bahnkurve des Punktes B demonstriert.
Die Bestimmung der Bahnkurve (Fragestellung a) ist mit einigen geometrischen Überlegungen nicht sehr schwierig. Die Kurve kann sinnvoll nur in Parameterdarstellung angegeben werden. Mit einem kartesischen Koordinatensystem mit dem Ursprung im Punkt C erhält man:
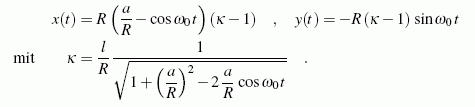
Zur Beantwortung der Fragestellung b müssen die beiden Funktionen x(t) und y(t) nach t abgeleitet werden. Das ist nicht schwierig, aber etwas mühsam. Deshalb wird hier darauf verzichtet, weil zur grafischen Darstellung das über TM-interaktiv verfügbare Programm "Funktionen analysieren" genutzt werden soll, mit dem numerisches Differenzieren möglich ist, so dass auch die Fragestellung c damit zu beantworten ist.
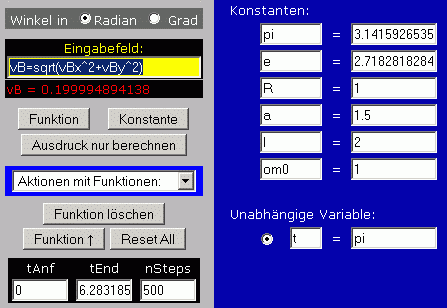
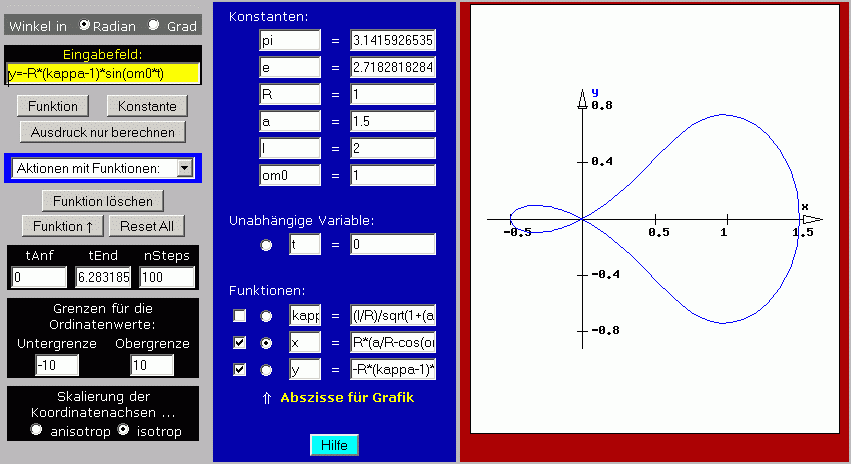
Nach dem Start des Programms werden zunächst die Problemparameter R, a, l und ω0 als Konstanten R, a, l und om0 definiert. Die unabhängige Variable wird auf t umgestellt, danach können die Funktionen kappa, x und y definiert werden (kappa als erste Funktion, weil x und y von dieser Funktion abhängig sind). Im nachfolgenden Bildschirm-Schnappschuss sieht man die zuletzt definierte Funktion noch im gelben Eingabefeld links oben.
Für die grafische Darstellung sollten noch folgende Einstellungen geändert werden: tEnd sollte auf 2*pi gesetzt werden (ein kompletter Umlauf), und unten links sollte die "Skalierung der Koordinatenachsen" von "anisotrop" auf "isotrop" umgestellt werden, weil die beiden Koordinatenachsen x und y gleiche (Längen-)Dimensionen haben. Das "Häkchen" vor der Funktion kappa sollte entfernt werden, weil diese nicht dargestellt werden soll. Und weil y(x) gezeichnet werden soll, muss der Radiobutton, der die "Abszisse für Grafik" kennzeichnet, vor dem x aktiviert werden.
Nach diesen Vorarbeiten wird im Auswahlfeld "Aktionen mit Funktionen" das Angebot "Grafische Darstellung" angeklickt, und der Bildschirm sollte so aussehen:
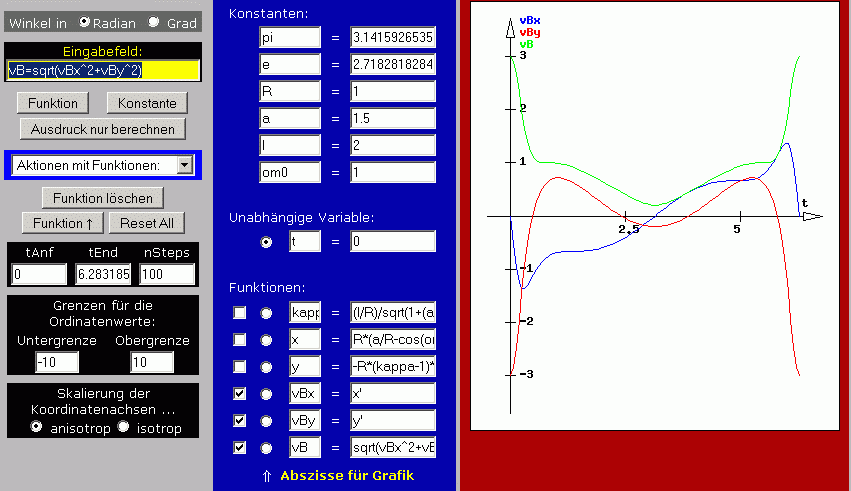
Fragestellung b: Für die Berechnung der Geschwindigkeiten werden drei zusätzliche Funktionen definiert: vBx = x' und vBy = y' sind die ersten Ableitungen der beiden Koordinaten nach der unabhängigen Variablen t (Geschwindigkeitskomponenten). "Wurzel aus der Summe der Quadrate der Geschwindigkeitskomponenten" ist dann die Geschwindigkeit vB des Punktes B. Die Definition dieser Funktionen sieht man im folgenden Bildschirm-Schnappschuss in der Mitte unten, die zuletzt eingegebene Funktion vB auch noch im gelben Eingabefeld links oben.
Für die graphische Darstellung der drei Funktionen vBx(t), vBy(t) und vB(t) werden folgende Einstellungen vorgenommen: Für die "Skalierung der Koordinatenachsen" wird (unten links) wieder "anisotrop" gewählt, weil mit Zeit und Geschwindigkeit unterschiedliche Größen abgebildet werden. Die "Abszisse für Grafik" wird wieder auf t umgestellt, und die Häkchen vor den Funktionen kappa, x und y werden entfernt, dafür vor den Funktionen vBx, vBy und vB gesetzt. Nun wird im Auswahlfeld "Aktionen mit Funktionen" wieder "Grafische Darstellung" angeklickt, und der Bildschirm sollte so aussehen:
|
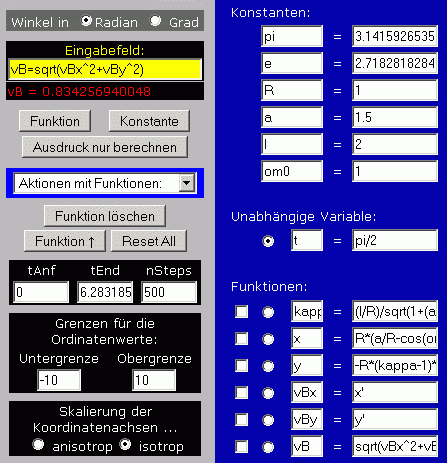
Fragestellung c: Man könnte einfach im Auswahlfeld "Aktionen mit Funktionen" das Angebot "Wertetabelle" anklicken und die beiden gefragten Geschwindigkeiten für die Zeitpunkte t = pi/2 (Punkt F) und t = pi/2 (Punkt E) ablesen. Weil aber numerisch differenziert werden muss, sind die Werte bei einer Schrittweite, die sich für nSteps = 100 ergibt, recht ungenau (für die oben erzeugte grafische Darstellung ist dieser Standardwert natürlich ausreichend). Andererseits ist die Berechnung mit einer wesentlich größeren Schrittanzahl recht aufwendig. Deshalb wird folgender Weg beschritten: Für nSteps wird ein ausreichend großer Wert gewählt (nebenstehend sieht man dafür die Zahl 500). Weil nach Fragestellung c nur ausgewählte Punkte berechnet werden sollen (es muss keine aufwendige Wertetabelle für den gesamten Bereich erzeugt werden), kann der Aufwand sehr klein gehalten werden. Das realisiert man folgendermaßen: Für die "Unabhängige Variable" t wird ein Wert eingegeben. Rechts sieht man den Wert pi/2, das entspricht dem Erreichen des Punktes F. Danach wird für die immer noch im Eingabefeld stehende Funktion vB das Angebot "Ausdruck nur berechnen" angeklickt, und der Wert erscheint. Dies wird mit dem Wert pi für den Zeitpunkt, an dem die Kurbel den Punkt E passiert, wiederholt. Nachfolgend sieht man das Ergebnis:
|
|
| Empfehlung: Man besuche die Seite "Krümmungsradius und Krümmungskreis", auf der die Entstehung der folgenden Animation beschrieben wird: |