
Aufgabe
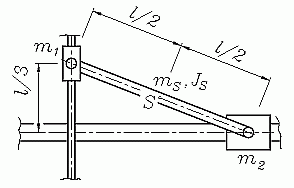
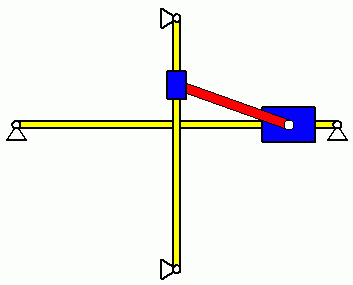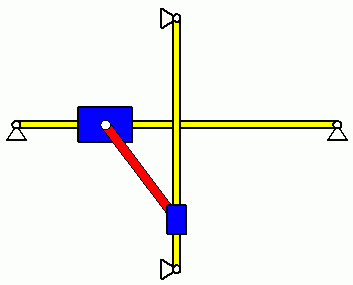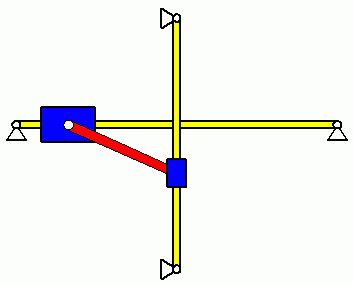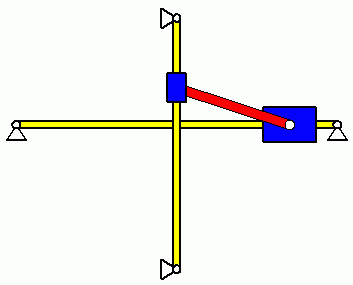
Zwei Massen m1 und m2 können auf einer vertikalen bzw. einer horizontalen Führung reibungsfrei gleiten. Sie sind durch eine starre Stange (Masse mS und Massenträgheitsmoment JS bezüglich des Schwerpunktes S) gekoppelt. Das gesamte System wird aus der skizzierten Lage ohne Anfangsgeschwindigkeit freigelassen.
Gegeben:
Das nur auf numerischem Wege zu gewinnende Bewegungsgesetz soll punktuell mit dem Energiesatz kontrolliert werden.
Bewegungs-Differenzialgleichung, Energiesatz
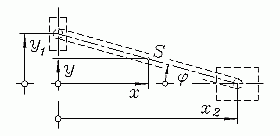
Die Aufgabe wird hier für verschiedene Fragestellungen mit Matlab gelöst. Zur Analyse des Bewegungsvorgangs muss zunächst das Anfangswertproblem gelöst werden (die Koordinate φ verfolgt die Bewegung der Verbindungsstange, siehe nebenstehende Skizze, die Herleitung der Differenzialgleichung wird im Kapitel "Kinetik starrer Körper" ausführlich behandelt):
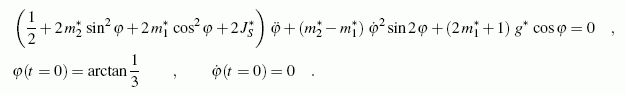
Wegen der vielfältigen Fehlerquellen wird im Kapitel "Kinetik starrer Körper" empfohlen, die Ergebnisse punktuell mit dem Energiesatz zu überprüfen.
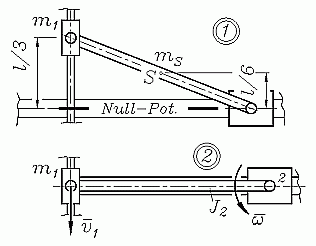
Die nebenstehende Skizze zeigt zwei Lagen des Systems, für die die Energiebilanz besonders einfach zu formulieren ist. Als Zustand 1 wird der Start der Bewegung und als Zustand 2 die horizontale Lage der Stange betrachtet. Mit dem Null-Potenzial in Höhe der horizontalen Führung hat das System nur im Zustand 1 potenzielle Energie. Im Zustand 2 befindet sich Masse 2 im Umkehrpunkt ihrer Bewegung, hat also keine kinetische Energie. Da sich damit auch der Bolzen 2 der Stange in Ruhe befindet, ist er der Momentanpol für die Stange, deren kinetische Energie damit besonders einfach formuliert werden kann. Dies wird im Kapitel "Kinetik starrer Körper" ausführlich beschrieben und führt über die Energiebilanz zu einer sehr einfachen Formel für die Winkelgeschwindigkeit der Verbindungsstange beim Passieren der Lage φ = 0:
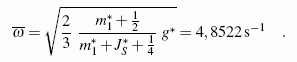
Die numerische Integration des Anfangswertproblems (hier mit erweiterter Aufgabenstellung ausführlich demonstriert) liefert das Bewegungsgesetz in Abhängigkeit von der Zeit als Wertetabelle. Die benötigte Nullstelle von φ(t) könnte man daraus durch Interpolation annähern, um danach aus der ebenfalls als Wertetabelle vorliegenden Funktion ω(t) auch durch Interpolation den speziellen ω-Wert (auch näherungsweise) zu gewinnen.
Für diese Aufgabe bietet Matlab allerdings mit der Event-Strategie eine effektive und natürlich viel bessere Lösungsmöglichkeit. Man kann den Algorithmen der numerischen Integration "Events" vorgeben, deren Eintreten bei der Integration überprüft wird, hier also zum Beispiel: Nulldurchgang der Funktion φ(t), und es werden der genaue Zeitpunkt des "Events" und die zugehörigen Funktionswerte φ und ω berechnet und zusätzlich abgeliefert. Dies wird nachfolgend gezeigt.
Lösung mit Matlab, Kontrolle mit dem Energiesatz
Das Anfangswertproblem 2. Ordnung muss für die Lösung mit Matlab in ein System 1. Ordnung umgeschrieben werden. Dafür wird eine neue Variable ω als Ableitung der Winkelkoordinate φ nach der Zeit eingeführt:
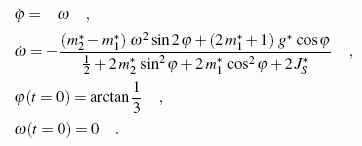
In dem folgenden Matlab-Script ist das Differenzialgleichungsssystem in der Function Dgl realisiert, die dem Verfahren zur numerischen Integration (ode45) beim Funktionsaufruf angezeigt wird. Bemerkungen zur Event-Strategie findet man nach dem Listing des Scripts.
global JSS m1S m2S gS
JSS = 1/12 ; m1S = 0.5 ; m2S = 2 ; gS = 29.43 ;
maxstep = 0.01 ; % ... fuer MaxStep-Option
phi0 = [asin(1/3) ; 0] ; tspan = [0 2] ; % Anfangswerte, Zeitintervall
options = odeset ('MaxStep' , maxstep , 'Events' , @Ereignis) ; % Event-Behandlung wird angekuendigt
[t phiphip te phiphipe ereig] = ode45 (@Dgl , tspan , phi0 , options) ;
phi = phiphip(:,1) ; phip = phiphip(:,2) ; % Sortieren der Ergebnisse
subplot(1,2,1) ; plot (t , phi) , grid on , title ('\phi(t)')
subplot(1,2,2) ; plot (t , phip) , grid on , title ('\omega(t)')
disp([' ']) ;
disp(['Rechnung mit MaxStep = ' , num2str(maxstep) , ':']) ;
for i=1:length(te) % Auswertung der "Events"
disp(['omega(t = ' , num2str(te(i)) , ') = ' , num2str(phiphipe(i,2))]) ;
end
disp(['phi (t_end = ' , num2str(t(end)) , ') = ' , num2str(phi(end))]) ; % Zusaetzliche Kontrolle:
disp(['omega(t_end = ' , num2str(t(end)) , ') = ' , num2str(phip(end))]) ; % Werte am Ende des Intervalls
% ===================================================================
function [value,isterminal,direction] = Ereignis (t,phiphip)
phi = phiphip(1) ;
value(1) = phi ; % Ereignis 1: "Nulldurchgang"
isterminal(1) = 0 ; % Kein Abbruch, aber registrieren ...
direction(1) = 0 ; % ... in jedem Fall (Hin- und Rueckweg)
% ============================================================
% Function, die die "rechte Seite" des Dgl.-Systems definiert:
function f = Dgl (t , phiphip)
global JSS m1S m2S gS
phi = phiphip(1) ;
omega = phiphip(2) ;
phiP = omega ;
zaehl = -((m2S-m1S)*omega^2*sin(2*phi)+(2*m1S+1)*gS*cos(phi)) ;
nenn = (0.5+2*m2S*(sin(phi))^2+2*m1S*(cos(phi))^2+2*JSS) ;
f = [phiP ; zaehl/nenn] ;
Die Passagen im vorstehenden Script, die sich auf die Matlab-Event-Strategie beziehen, sind farblich gekennzeichnet (hellblau die Ankündigung und Definition der Events, weiß die Auswertung der abgelieferten Informationen):
- Neben der obligatorischen "MaxStep-Option" (weil die Standardeinstellungen keine ausreichende Genauigkeit garantieren) kündigt die (hellblaue) "Events-Option" an, dass auf spezielle Ereignisse geachtet werden soll, und verweist auf ein Handle einer Function Ereignis (Name kann beliebig gewählt werden), die die "Events" definiert.
- Die Function Ereignis bekommt als Input die gleichen
Werte (Zeit und Vektor der Bewegungsgrößen) wie die Funktion für
die Definition der Differenzialgleichungen (hier: Dgl).
Die Function Ereignis muss für jedes Ereignis
drei Informationen abliefern (hier ist es nur ein Ereignis, eine Aufgabe
mit mehreren Ereignissen wird
hier
beschrieben):
- Eine "Nullfunktion" (hier auf Vektor value) definiert durch ihre Nullstelle das Ereignis (dies kann ein beliebiger Ausdruck sein, hier ist es nur die Variable phi, auf deren Nullstelle geachtet werden soll).
- Was soll beim Eintreten dieses Ereignisses geschehen? Die hier auf isterminal abgelieferte 0 bedeutet: Ereignis nur registrieren, Rechnung nicht abbrechen. Eine 1 würde Abbruch bedeuten, ein Beispiel, für das dies sinnvoll ist, findet man hier.
- Der dritte Parameter spezifiziert das Ereignis genauer: Die hier auf direction abgelieferte Null bedeutet, dass jeder Nulldurchgang als Ereignis registriert wird (eine 1 würde nur Nulldurchgänge von negativen in positive Werte registrieren, eine −1 nur Nulldurchgänge von positiven in negative Werte).
- Die ode45-Function liefert bei gesetzter Event-Option
neben den Wertetabellen für die Zeit und die Bewegungsgrößen
(hier: t und phiphip)
drei zusätzliche Ergebnisse (im Script weiß gekennzeichnet):
- Der Vektor te enthält alle Zeitpunkte, zu denen Ereignisse registriert worden sind (die Länge des Vektors entspricht der Anzahl der Ereignisse).
- Die Matrix phiphipe enthält alle Bewegungsgrößen zu diesen Zeitpunkten.
- Der Vektor ereig enthält die Informationen, welche Ereignisse eingetreten sind (hier gibt es nur ein Ereignis, deshalb steht dort auf allen Positionen eine 1).
- In einer ebenfalls weiß gekennzeichneten Schleife gibt das Script mit der disp-Function die Winkelgeschwindigkeiten zu den speziellen Zeitpunkten aus, an denen φ(t) einen Nulldurchgang hat.
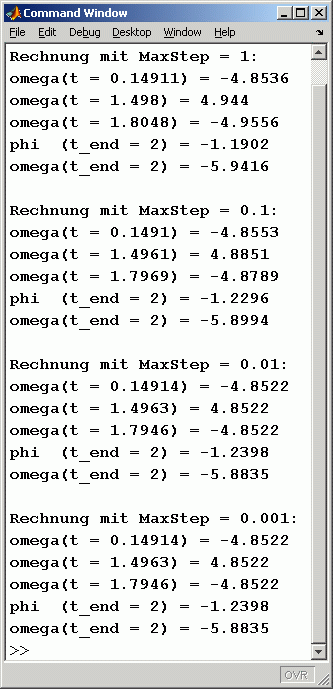
Die Rechnung wurde mehrmals mit unterschiedlichen MaxStep-Options durchgeführt. Die nebenstehend zu sehende Ausgabe in das Command Window zeigt, dass im Integrationsbereich drei Ereignisse registriert werden. Neben den "Ereignis-Winkelgeschwindigkeiten" werden auch die Endwerte für φ und ω ausgegeben. Man erkennt, dass die MaxStep-Option 0,01 offensichtlich für ausreichende Genauigkeit sorgt. Sowohl die Winkelgeschwindigkeiten als auch die Endwerte ändern sich bei feinerer MaxStep-Option nicht mehr.
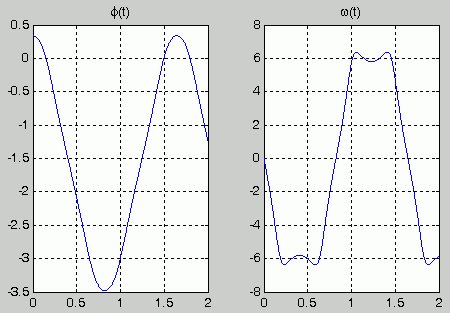
Die theoretischen Vorgaben werden bestätigt: Die Winkelgeschwindigkeiten beim Passieren der Lage φ = 0 entsprechen genau dem nach dem Energiesatz zu erwartenden Wert (die Vorzeichen entsprechen der mit der Definition der Koordinate φ festgelegten positiven Drehrichtung). Die nachfolgend zu sehenden kinematischen Diagramme zeigen, dass die Ereignisse tatsächlich den Nullstellen der Funktion φ(t) zuzuordnen sind, und die ausgegebenen Winkelgeschwindigkeiten entsprechen ebenfalls den Werten, die das Diagramm anzeigt:
Plausibilität der Kinematik, Animation
Die oben zu sehenden Diagramme φ(t) und ω(t) sind schwierig zu interpretieren. Immerhin zeigt sich bereits der zu erwartende periodische Verlauf, die Erfüllung der Anfangsbedingungen und die erwartete Zuordnung spezieller ω-Werte zu den Nulldurchgängen der Funktion φ(t). Eine Vorstellung vom zu erwartenden Bewegungsverlauf hat man allerdings eher für die beiden Gleitsteine, deren Bewegungsgesetze deshalb nachfolgend noch berechnet werden.
Außerdem ist aus der Kinematik bekannt, dass sich der Mittelpunkt der Verbindungsstange eines Doppelschiebers auf einer Kreisbahn bewegt. Auch dies wird mit der nachfolgenden Testrechnung überprüft.
Die für die Darstellung benötigten Koordinaten sind über die hier angegebenen Zwangsbedingungen aus der Funktion φ(t) leicht zu berechnen. Sie lauten in dimensionsloser Form (bezogen auf die Länge l der Verbindungsstange):
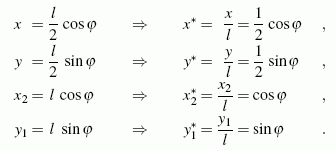
Das Matlab-Script enthält nur noch die wesentlichen Passagen des oben gezeigten Scripts, mit denen die graphische Darstellung der gewünschten Funktionen gelingt:
global JSS m1S m2S gS
JSS = 1/12 ; m1S = 0.5 ; m2S = 2 ; gS = 29.43 ;
phi0 = [asin(1/3) ; 0] ; tspan = [0 2] ; % Anfangswerte, Zeitintervall
options = odeset ('MaxStep' , 0.01) ;
[t phiphip] = ode45 (@Dgl , tspan , phi0 , options) ;
phi = phiphip(:,1) ; phip = phiphip(:,2) ; % Sortieren der Ergebnisse
xS = 0.5*cos(phi) ; yS = 0.5*sin(phi) ; % Mittelpunkt der Verbindungsstange
x2S = cos(phi) ; y1S = sin(phi) ; % Gleitsteine
subplot(1,3,1) ; plot (t , x2S) , grid on , title ('x_2^{\ast}(t)')
subplot(1,3,2) ; plot (t , y1S) , grid on , title ('y_1^{\ast}(t)')
subplot(1,3,3) ; plot (xS , yS ) , grid on , title ('y(x)') , axis equal
% ============================================================
% Function, die die "rechte Seite" des Dgl.-Systems definiert:
function f = Dgl (t , phiphip)
global JSS m1S m2S gS
phi = phiphip(1) ;
omega = phiphip(2) ;
phiP = omega ;
zaehl = -((m2S-m1S)*omega^2*sin(2*phi)+(2*m1S+1)*gS*cos(phi)) ;
nenn = (0.5+2*m2S*(sin(phi))^2+2*m1S*(cos(phi))^2+2*JSS) ;
f = [phiP ; zaehl/nenn] ;
Die Graphik-Ausgabe des Scripts zeigt die drei Diagramme:
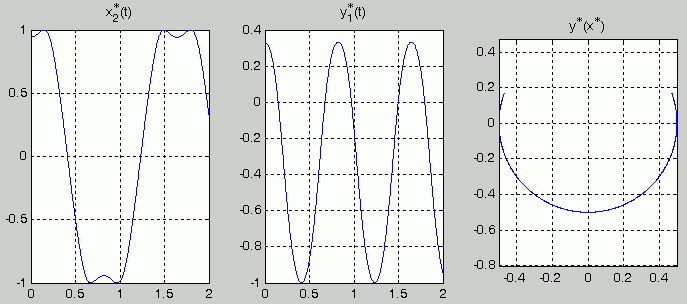
Interpretation der Kontrollrechnung:
- Der Mittelpunkt der Verbindungsstange bewegt sich (wie erwartet) auf einer Kreisbahn (rechtes Bild). Dass der Kreis nicht geschlossen ist, liegt daran, dass der sich vertikal bewegende Gleitstein nicht seine kinematisch mögliche Höchstlage erreicht, sondern maximal bis zu seiner Startlage kommt.
- Der sich vertikal bewegende Gleitstein führt (wie erwartet) eine regelmäßige (annähernd harmonische) Schwingung aus (mittleres Bild).
- Interpretationsbedürftig sind die "kleinen Dellen" in der Nähe der Maximalausschläge des sich horizontal bewegenden Gleitsteins (linkes Bild): Der Maximalausschlag wird jeweils erreicht, wenn der andere Gleitstein die Nulllage passiert. Weil die Bewegung dieses Gleitsteins nach oben nur eine vergleichsweise kurze Strecke ist (im Vergleich zur Bewegung bis zum unteren Totpunkt), wird der sich horizontal bewegende Gleitstein in relativ kurzem zeitlichen Abstand zweimal zu seiner Extremlage geführt. In der nebenstehend zu sehende Animation der Bewegung äußert sich das in dem kurzen "Hin-und-Her" in der Nähe seiner Extremlagen.
Download
Die oben zu sehenden Matlab-Scripts stehen als BolzenkraefteEv.m und BolzenkraefteEv2.m zum Download zur Verfügung.
