
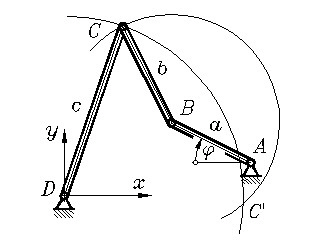
Viergelenkkette
Eine Viergelenkkette wird definiert durch die Lage der beiden Fixpunkte A und B (z. B. durch Angabe der Koordinaten xA und yA des Punktes A in einem Koordinatensystem mit dem Ursprung in B) und die Längen der drei Glieder a, b und c.
Die beliebige Lage der Viergelenkkette soll durch den Winkel φ beschrieben werden, der die Lage des Getriebegliedes beschreibt, das im Punkt A fixiert ist. Dann gilt für die Lage des Punktes B:
xB = xA − a cos φ , yB = yA + a sin φ .
Der Punkt C kann nur in einem der beiden Schnittpunkte der Kreise um D (mit dem Radius c) und B (mit dem Radius b) liegen.
Hier findet man eine interaktive Animation von Viergelenkkettten mit beliebigen Abmessungen.
Bei der Berechnung der Koordinaten für den Punkt B können sich zwei (reelle) Lösungen ergeben, eine (Doppel-)Lösung (die beiden Kreise berühren sich) oder keine (reelle) Lösung. Grund für den leztgenannten Fall kann eine unmögliche (durch φ beschriebene) Lage der Viergelenkkette oder eine unmögliche Viergelenkkette sein. Die Probleme, die damit und mit der Entscheidung, welche der beiden Lösungen verwendet werden muss, werden im Abschnitt "Koppelgetriebe" im Kapitel "Kinematik des Punktes" ausführlich diskutiert.
In Abhängigkeit von den Abmessungen a, b und c der drei Glieder und der Lage der beiden Lagerpunkte A und D können die beiden gelagerten Glieder in ihren Bewegungsmöglichkeiten eingeschränkt sein. Man nennt sie Kurbeln, wenn sie eine komplette Kreisbewegung ausführen können, ansonsten Schwingen.
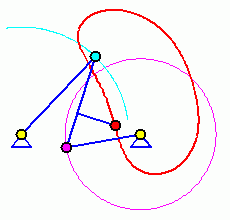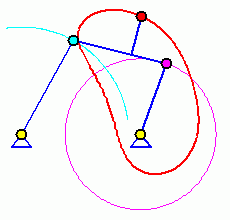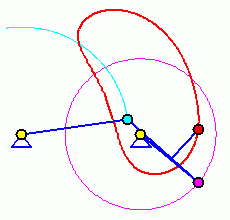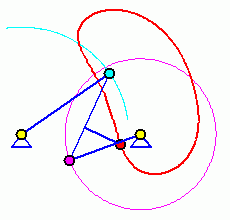
Kurbelschwinge
Kurbelschwinge
Bei einer Kurbelschwinge erzeugt die (Antriebs-)Kurbel bei ihrem kompletten Umlauf eine schwingende Bewegung des anderen Gliedes, der Schwinge.
Der violette Punkt der Kurbel bewegt sich auf einem Kreis, während sich der hellblaue Punkt der Schwinge auf einem Kreisbogen hin und her bewegt. Der rote so genannte Koppelpunkt ist starr mit der Koppel, die zwischen Kurbel und Schwinge liegt, verbunden. Er bewegt sich auf der rot gezeichneten Koppelkurve.
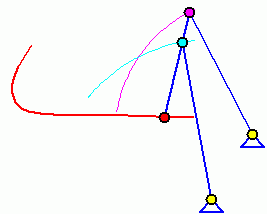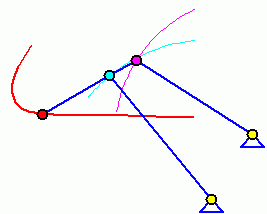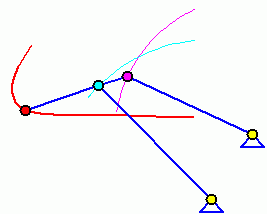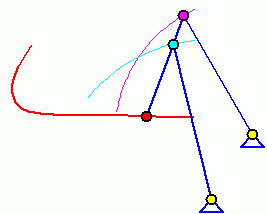
Doppelschwinge (Wippkran-Mechanismus)
Doppelschwinge
Bei einer Doppelschwinge können die beiden gelagerten Glieder nur schwingende Bewegungen ausführen (die von dem violetten bzw. dem hellblauen Punkt erreichbaren Punkte sind als Bahnkurven eingezeichnet).
Das Koppelgetriebe, bei der der mit der Koppel starr verbundene rote Punkt auf der durch B und C definierten Geraden liegt, ist mit den hier dargestellten Abmessungen ein Beispiel für das Erzeugen einer speziell gewünschten Bahnkurve. Man erkennt, dass diese in einem gewissen Bereich eine fast ideale horizontale Gerade ist. Das wird für so genannte Wippkräne ausgenutzt, bei denen die anhängende Last bei Transport in der Horizontalen in diesem Bereich weder gehoben noch gesenkt wird, so dass für diese Bewegung nur eine minimale Antriebsleistung erforderlich ist.
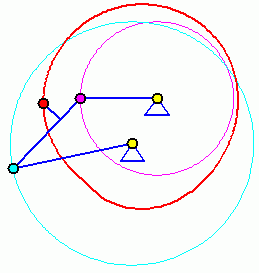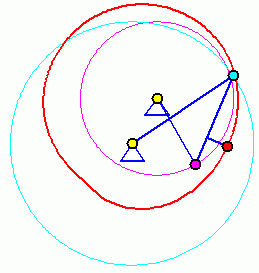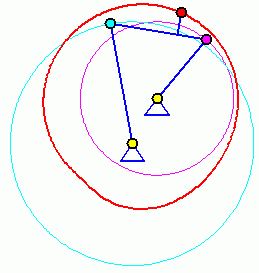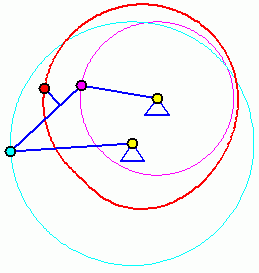
Doppelkurbel
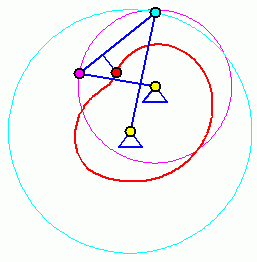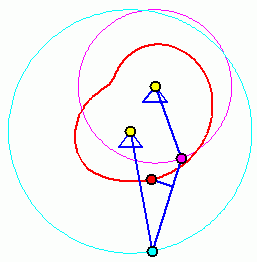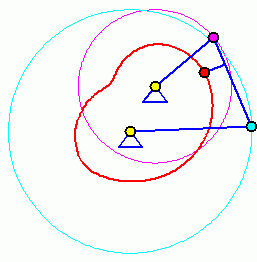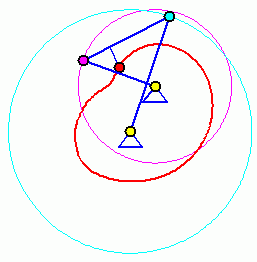
Doppelkurbel
Doppelkurbel
Bei einer Doppelkurbel können beide gelagerten Glieder eine komplette Kreisbewegung ausführen. Die beiden Animationen zeigen, dass die Bewegung (und damit auch die Bahnkurve eines Koppelpunktes) von der Anfangsstellung abhängig ist. Für die Für die beiden völlig identischen Getriebe sind zwei Anfangstellungen möglich (entsprechend der beiden Punkte C und C', im Bild "Viergelenkkette"), die zu völlig unterschiedlichen Bewegungen führen.
Animationen erzeugen mit GeoGebra
Mit der kostenlosen Mathematik-Software GeoGebra können Animationen von Mechanismen der Art, wie sie hier behandelt werden, auf relativ einfache Weise erzeugt und manipuliert werden.
Dies wird für den nebenstehend skizzierten Mechanismus (vgl. Seite "Theo Jansens Strandbeest-Mechanismus") sehr anschaulich demonstriert mit der von Karl Hovekamp erzeugten GeoGebra-Datei strandbeest-mechanismus.ggb, die zum Download verfügbar ist. Sie gestattet während der Animation die Änderung aller Längen der Getriebeglieder (in sinnvollen Grenzen), und man sieht sofort die Auswirkungen auf die Bewegung.
Weil ein voll funktionsfähiges GeoGebra-Applet aber auch im Internet-Browser lauffähig ist, kann man sich das nach Klick auf das nebenstehende Bild ansehen, ohne die Software auf dem eigenen Computer zu installieren. Allerdings muss dafür (und sollte eigentlich sowieso) auf Ihrem Computer Java installiert sein ("Java Runtime Environment"). Dies kann kostenlos bezogen werden von http://www.java.com.
