Problem

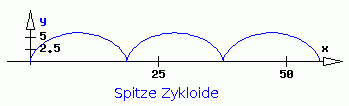
Ein Rad mit dem Radius R rollt (ohne zu gleiten) mit der konstanten Geschwindigkeit v₀ auf der Horizontalen. Für einen Punkt A im Abstand a vom Radmittelpunkt sollen die Bahnkurve und die Bahngeschwindigkeit für drei komplette Umdrehungen des Rades ermittelt werden.

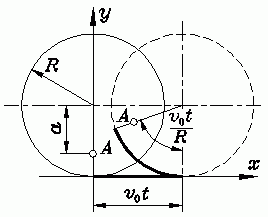
Das Koordinatensystem wird (wie skizziert) so gelegt, dass sich das Rad zur Zeit  t = 0  bei  x = 0  befindet und der Punkt A senkrecht unter dem Radmittelpunkt liegt.

Nach einer Zeit t (gestrichelt gezeichnet) hat das Rad den Weg v₀ t zurückgelegt und die gleiche Strecke auf dem Umfang abgewälzt (fett gezeichnet), so dass der Punkt A unter dem eingezeichneten Winkel ("Bogen/Radius") zu finden ist. Für seine Lage zum Zeitpunkt t liest man aus der Skizze folgende Parameterdarstellung der Bewegung (bzw. der Bahnkurve) ab:

Seine Bahngeschwindigkeit errechnet man aus den Ableitungen von x bzw y nach der Zeit t:

Lösung

Lösung interaktiv mit dem Programm "Funktionen analysieren":

Animation, erzeugt mit Maple: