Aufgabe

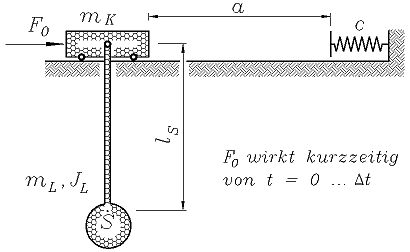
Eine Laufkatze (Masse m_K) trägt eine Last (Masse einschließlich Anhängevorrichtung: m_L, Massenträgheitsmoment bezüglich des Schwerpunktes S: J_L). In der skizzierten Ruhelage beginnt für eine kurze Zeit Δt die konstante Antriebskraft F₀ zu wirken, die danach wieder abgeschaltet wird. Nach dem Zurücklegen der Strecke a stößt die Laufkatze auf einen elastischen Puffer (Federzahl c).

Die Bewegung von Laufkatze und Last soll, beginnend aus der Ruhelage, für die ersten 10 Sekunden analysiert werden.

Gegeben:

m_K = 100 kg ;  J_L = 400 kgm² ;  l_S = 4 m ;  F₀ = 2000 N ;
m_L = 500 kg ;  c = 200000 N/m ;  Δt = 1 s ;  a = 5 m .

Die Aufgabe wird in den Kapiteln "Prinzipien der Mechanik" und "Verifizieren von Computerrechnungen" behandelt.

Bewegungs-Differenzialgleichungen

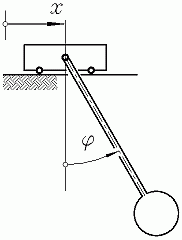
Die Besonderheit dieser Aufgabe besteht in dem Eintreten von "Ereignissen" (Abschalten der Antriebskraft, Zu- und Abschalten einer Feder). Man erfasst sie, indem an die Stelle der Kraft F₀ die zeitabhängige Kraft F_t tritt und die Federkonstante c durch c_t ersetzt wird:

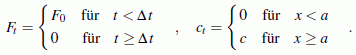
Unter Verwendung der nebenstehend skizzierten Koordinaten gelten folgende Bewegungs-Differenzialgleichungen (die ausführlich kommentierte Herleitung findet man im Kapitel "Prinzipien der Mechanik"):

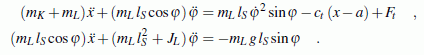
Dieses Differenzialgleichungssystem hat aus mathematischer Sicht alle denkbaren unangenehmen Eigenschaften: Es ist hochgradig nichtlinear, in den Beschleunigungsgliedern gekoppelt, und es sind ein zeitabhängiges und ein wegabhängiges Ereignis zu berücksichtigen. Die Lösung kann nur numerisch gelingen.

Numerische Lösung, Verifizieren der Ergebnisse

Entsprechend den im Kapitel "Verifizieren von Computerrechnungen" gegebenen Empfehlungen wird das Problem mit unterschiedlichen Software-Produkten gelöst. Die Genauigkeit der numerischen Berechnungen wird auf zwei Wegen überprüft: Mehrfachrechnungen mit verschiedenen Schrittweiten (trotz Verwendung eines Algorithmus mit automatischer Schrittweitensteuerung) geben ein Gefühl dafür, ob die Schrittweitenwahl sinnvoll ist, und das Erzeugen einer Kontrollfunktion überprüft die gesamte Rechnung vom Berechnungsmodell bis zur Lösung. Schließlich wird mit einer Animation ein Gefühl dafür erzeugt, ob das berechnete Bewegungsgesetz sinnvoll sein kann.

• Einfache Berechnung mit Matlab: Da für die numerische Lösung eine Function bereitgestellt werden muss, die das Differenzialgleichungssystem definiert, können dort die Abfragen eingebaut werden, ob die Antriebskraft gerade wirkt und ob gerade Kontakt mit der Feder besteht. Diese besonders einfache Realisierung von "Ereignissen" ist aber prinzipiell "nicht ganz sauber", weil in jedem Integrationsschritt die Differenzialgleichungen mehrfach ausgewertet werden müssen. Eine Änderung der Parameter innerhalb eines Integrationsschrittes kann den Algorithmus der automatischen Schrittweitensteuerung so ungünstig beeinflussen, dass die Rechnung kollabiert (ein einfaches Beispiel dafür findet man hier).
  Für das Laufkatzen-Problem funktioniert jedoch diese "schnelle, aber nicht ganz saubere Lösung" sehr gut, man findet sie auf der Seite "Laufkatze mit pendelnder Last - einfache Berechnung mit Matlab".
• Berechnung mit "Event-Strategie", Verifizieren der Ergebnisse mit einer Kontrollfunktion: Für die korrekte Berücksichtigung von "Ereignissen" bietet Matlab die "Event-Strategie" an, mit der für die vorab zu definierenden "Events" die genaue Position und der genaue Zeitpunkt ermittelt werden, so dass darauf entsprechend reagiert werden kann. Dies wird (zusätzlich mit dem Verifizieren der Ergebnisse mit einer Kontrollfunktion) auf der Seite "Laufkatze - Berechnung mit der Event-Strategie" demonstriert.
• Berechnung mit Simulink (einschließlich Kontrollfunktion): Eine grundsätzlich andere Definition des Differenzialgleichungssystems wird mit Simulink verfolgt. Die damit erzielte sehr wirkungsvolle Verifizierung der Ergebnisse der oben beschriebenen Berechnungen wird auf der Seite "Laufkatze - Berechnung mit Simulink" gezeigt.
• Verifizieren der Ergebnisse mit dem Runge-Kutta-Algorithmus 4. Ordnung (einschließlich Kontrollfunktion): Eine Rechnung mit dem klassischen Runge-Kutta-Verfahren 4. Ordnung mit konstanter Schrittweite kann eine sehr einfache Realisierung der Ereignisse verwenden. Das Verfahren ist in der Regel recht robust und damit immer als Kontrollrechnung geeignet, die für das hier betrachtete Problem auf der Seite Laufkatze - Berechnung mit Runge-Kutta 4. Ordnung gezeigt wird.
• Simulation der Bewegung: Schließlich liefert die Simulation der berechneten Bewegungsgesetze eine gutes Gefühl dafür, dass die zunächst etwas merkwürdig erscheinende Bewegung der Laufkatze durchaus korrekt sein kann.

Ergebnisse, Animation der Bewegung

Alle oben beschriebenen Rechnungen liefern die nachfolgend zu sehenden Bewegungsgesetze x(t) (Laufkatze) und φ(t) (pendelnde Last):

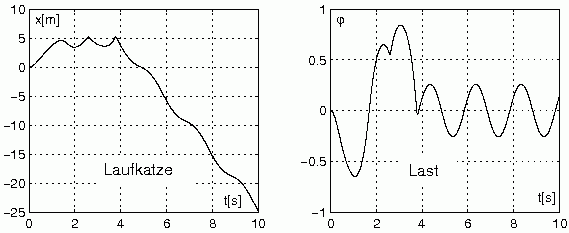
Die Laufkatze bewegt sich erwartungsgemäß zunächst nach rechts und tritt nach etwa t = 4s den Rückweg an. Die Last schwingt nach dem Start der Bewegung relativ weit aus, um dann auf dem Rückweg eine recht regelmäßige Schwingung auszuführen. Es lohnt sich, speziell das Weg-Zeit-Gesetz für die Laufkatze etwas genauer zu analysieren.

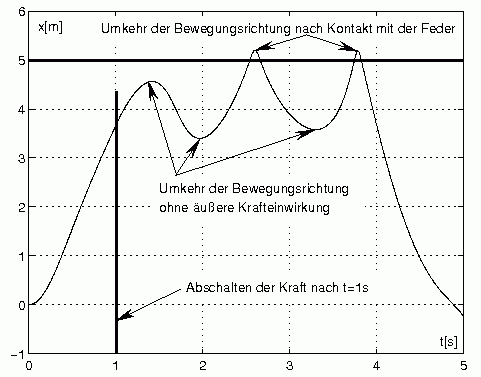
Die nachfolgende Abbildung links zeigt einen Zoom in das Bewegungsgesetz der Laufkatze. Bevor sie ihren Rückweg antritt, gibt es insgesamt fünfmal eine Umkehr der Bewegungsrichtung, erstmals kurz nach dem Abschalten der Antriebskraft deutlich vor dem Erreichen der Feder.

Es folgt aber unmittelbar eine weitere Umkehr (wie die erste ohne äußere Krafteinwirkung), so dass es doch zum Anschlag an die Feder kommt. Nach dem (ersten) Kontakt mit der Feder gibt es eine weitere (die dritte) Umkehr der Bewegungsrichtung ohne äußere Krafteinwirkung, so dass es zu einem zweiten Anschlag an die Feder kommt, der dann eine recht gleichmäßig verlaufende Bewegung (Rückweg) einleitet.

Was im Diagramm noch etwas überraschend erscheint, wird mit der unten rechts zu sehenden Animation der Bewegung verständlich: Man sieht, wie die schwingende Last auf die Laufkatze einwirkt und Änderungen der Bewegungsrichtung auch ohne äußere Krafteinwirkung erzwingt:

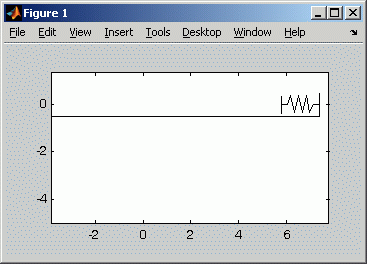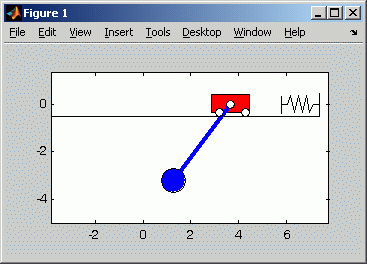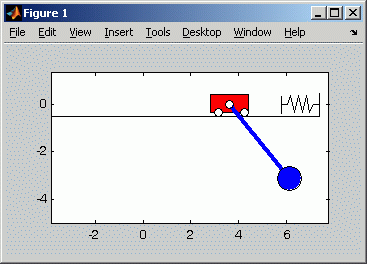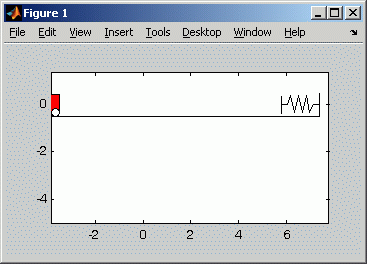
Die Animation zeigt die Bewegung von Laufkatze und Last etwa für den Zeitbereich, der im links zu sehenden Diagramm als Bewegungsgesetz der Laufkatze dargestellt ist.