Aufgabe

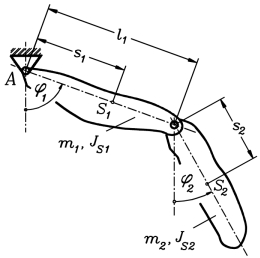
Ein Doppelpendel wird definiert durch die beiden Pendelmassen m₁ und m₂, die auf die jeweiligen Schwerpunkte bezogenen Massenträgheitsmomente J_S1 und J_S2, die Schwerpunktabstände von den Drehpunkten s₁ und s₂ und den Abstand l₁ der beiden Drehpunkte voneinander.

Die Bewegung soll durch die Funktionen φ₁(t) und φ₂(t) beschrieben werden, die für das Zeitintervall t = 0 ... 10 s zu berechnen sind.

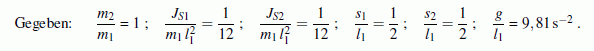
Die Aufgabe wird in den Kapiteln "Prinzipien der Mechanik" und "Verifizieren von Computerrechnungen" behandelt.

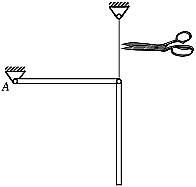
Die gegebenen Werte gelten für zwei schlanke Stäbe gleicher Masse und gleicher Länge. Sie sollen aus der nebenstehend skizzierten Anfangslage ohne Anfangsgeschwindigkeiten freigelassen werden, so dass folgende Anfangsbedingungen gelten:

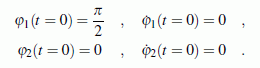
Bewegungs-Differenzialgleichungen

Unter Verwendung der in der Aufgabenstellung skizzierten Koordinaten gelten folgende Bewegungs-Differenzialgleichungen (die ausführlich kommentierte Herleitung findet man im Kapitel "Prinzipien der Mechanik"):

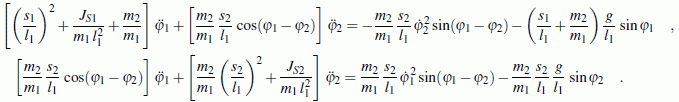
Dieses Differenzialgleichungssystem ist hochgradig nichtlinear und in den Beschleunigungsgliedern gekoppelt. Die Lösung kann nur numerisch gelingen.

Numerische Lösung, Verifizieren der Ergebnisse

Entsprechend den im Kapitel "Verifizieren von Computerrechnungen" gegebenen Empfehlungen wird das Problem mit unterschiedlichen Software-Produkten gelöst. Die Genauigkeit der numerischen Berechnungen wird auf zwei Wegen überprüft: Mehrfachrechnungen mit verschiedenen Schrittweiten (trotz Verwendung eines Algorithmus mit automatischer Schrittweitensteuerung) geben ein Gefühl dafür, ob die Schrittweitenwahl sinnvoll ist, und das Erzeugen einer Kontrollfunktion überprüft die gesamte Rechnung vom Berechnungsmodell bis zur Lösung. Schließlich wird mit einer Animation versucht, ein Gefühl dafür zu erzeugen, ob das berechnete Bewegungsgesetz sinnvoll sein kann, was allerdings bei dieser chaotischen Bewegung nur sehr bedingt gelingt.

• Einfache Berechnung mit Matlab: Die Rechnung wird mit dem Matlab-Standard-Solver ode45 durchgeführt. Man findet die Rechnung auf der Seite "Doppelpendel, Berechnung mit Matlab". Eine Modifikation dieses Matlab-Scripts, das eine ganz einfache Animation der Bewegung erzeugt, findet man auf der Seite "Doppelpendel - einfache Animation mit Matlab".
• Berechnung mit Matlab, Kontrolle mit Runge-Kutta, Schrittweitenkontrolle, Berechnung einer Kontrollfunktion: Die Rechnung wird parallel mit dem Matlab-Standard-Solver und dem klassischen Runge-Kutta-Verfahren 4. Ordnung durchgeführt. Zusätzlich wird die Gesamtenergie im System als Kontrollfunktion berechnet und graphisch dargestellt. Durch Mehrfachrechnung mit Kontrolle der Endwerte wird die geeignete Schrittweite ermittelt. Man findet die Rechnung auf der Seite "Doppelpendel, Berechnung mit zwei Verfahren".
• Berechnung mit Simulink (einschließlich Kontrollfunktion): Eine grundsätzlich andere Definition des Differenzialgleichungssystems wird mit Simulink verfolgt. Die damit erzielte sehr wirkungsvolle Verifizierung der Ergebnisse der oben beschriebenen Berechnungen wird auf der Seite "Doppelpendel - Berechnung mit Simulink" gezeigt.
• Simulation der Bewegung: Schließlich liefert die Simulation der berechneten Bewegungsgesetze (in diesem Fall nur eingeschränkt) ein Gefühl dafür, ob die Bewegung korrekt sein kann.
• Grenzen der Berechnung: Die Simulation der chaotischen Bewegung eines Doppelpendels ist nur für sehr kleine Zeitbereiche möglich und sinnvoll. Auf der Seite Doppelpendel - Grenzen der Simulation werden die Grenzen dafür ausgelotet.

Ergebnisse

Alle oben beschriebenen Rechnungen liefern die nachfolgend zu sehenden Bewegungsgesetze:

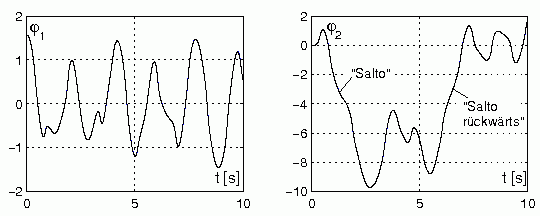
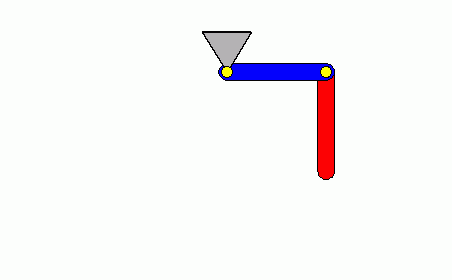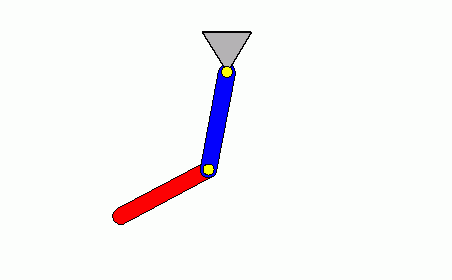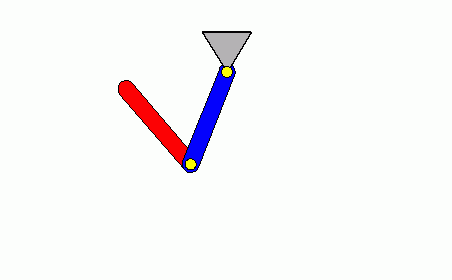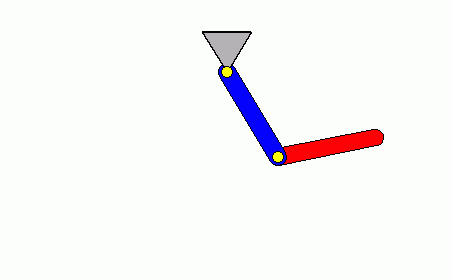
Die recht bizarren Funktionsverläufe spiegeln den tatsächlich außerordentlich komplizierten Bewegungsablauf eines solchen Doppelpendels wider. Während das obere Pendel eine recht unregelmäßige Schwingung ausführt, beginnt das untere Pendel mit einem "Salto", dem bald darauf ein "Salto rückwärts" folgt.

Die nebenstehend zu sehende Animation zeigt genau diese Bewegung für den untersuchten Zeitbereich.