
|
Doppelpendel - Matlab (mit Kontrollen)
|
 Achtung, hier wird geschummelt!
Achtung, hier wird geschummelt!
|
|||||
|
Aufgabe
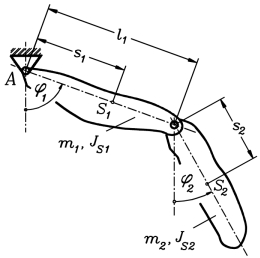
Ein Doppelpendel wird definiert durch die beiden Pendelmassen m1 und m2, die auf die jeweiligen Schwerpunkte bezogenen Massenträgheitsmomente JS1 und JS2, die Schwerpunktabstände von den Drehpunkten s1 und s2 und den Abstand l1 der beiden Drehpunkte voneinander.
Die Bewegung soll durch die Funktionen φ1(t) und φ2(t) beschrieben werden, die für das Zeitintervall t = 0 ... 10 s zu berechnen sind.
Die Aufgabe wird in den Kapiteln "Prinzipien der Mechanik" und "Verifizieren von Computerrechnungen" behandelt.
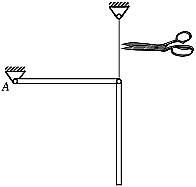
Die gegebenen Werte gelten für zwei schlanke Stäbe gleicher Masse und gleicher Länge. Sie sollen aus der nebenstehend skizzierten Anfangslage ohne Anfangsgeschwindigkeiten freigelassen werden, so dass folgende Anfangsbedingungen gelten:
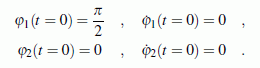
Bewegungs-Differenzialgleichungen, Vorbereitung der Matlab-Rechnung
Unter Verwendung der in der Aufgabenstellung skizzierten Koordinaten gelten folgende Bewegungs-Differenzialgleichungen (die ausführlich kommentierte Herleitung findet man im Kapitel "Prinzipien der Mechanik"):
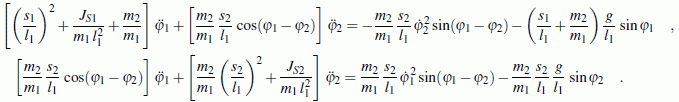
Das Anfangswertproblem soll mit zwei verschiedenen Verfahren gelöst werden: Matlab-Standard-Solver ode45 (Dormand-Prince-Verfahren mit variabler Schrittweite) und klassisches Runge-Kutta-Verfahren 4. Ordnung mit konstanter Schrittweite (Function rk4, die mit dem im Kapitel "Kinetik des Massenpunktes" gelisteten Formelsatz arbeitet).
Beide Verfahren erwarten ein Differenzialgleichungssystem 1. Ordnung. Deshalb werden die beiden neuen Variablen ω1 und ω2 eingeführt:
Damit kann das Anfangswertproblem so formuliert werden, wie man es dem Matlab-ode45-Solver anbieten kann:
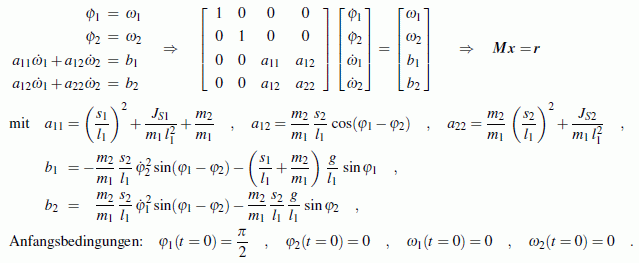
Die Function rk4 erwartet das nach den ersten Ableitungen aufgelöste System, das mit den oben bereits angegebenen Abkürzungen a11, a12, a22, b1 und b2 zum Beispiel so formuliert werden kann (auch die Anfangsbedingungen gelten wie oben formuliert):
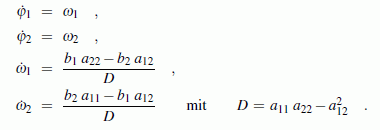
Berechnungsstrategie, Kontrollen
Die Berechnung wird mit dem Standard-Solver von Matlab (ode45) ausgeführt. Dieser steuert die Schrittweite automatisch. Anschließend wird die Runge-Kutta-Rechnung mit der gleichen Anzahl von Schritten ausgeführt, die ode45 berechnet hat. Die Rechnungen werden mit folgenden Strategien kontrolliert:
- Die Ergebnisse beider Verfahren werden graphisch in einem Fenster übereinander gezeichnet, so dass Abweichungen sofort zu erkennen sind.
- Die Werte am Ende des Integrationsintervalls für φ1 und φ2 werden ausgegeben. Die Rechnung wird mehrfach durchgeführt, wobei die zur Schrittweitensteuerung vorgesehene "MaxStep"-Option solange verkleinert wird, bis die Endwerte stabil sind.
- Entsprechend der Empfehlung im Kapitel "Verifizieren
von Computerrechnungen" wird eine Kontrollfunktion berechnet
und graphisch dargestellt. Dort wird für die Gesamtenergie,
die im System zu jedem Zeitpunkt gespeichert ist,
folgender Ausdruck hergeleitet (hier in dimensionsloser
Form aufgeschrieben, das Null-Potenzial liegt auf der
Höhe des Aufhängepunktes):
Dieser komplizierte Ausdruck muss für jeden Satz der Bewegungsgrößen φ1, φ2, ω1, ω2 eines beliebigen Zeitpunkts t den gleichen Wert ergeben. Es ist die Gesamtenergie, die bereits am Anfang der Bewegung (als potenzielle Energie) vorhanden ist:
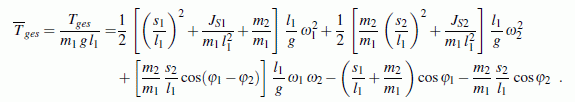
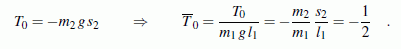
Matlab-Script
Weil das Bewegungs-Differenzialgleichungssystem in den Beschleunigungsgliedern gekoppelt ist, entsteht nach dem Umschreiben auf ein System 1. Ordnung auf der linken Seite des Differenzialgleichungssystems eine "Massenmatrix" M. Die Matlab-Solver können damit umgehen, man muss nur über die "options", die dem Solver (hier: ode45) übergeben werden, ankündigen, dass eine gesonderte Function diese Matrix beschreibt (hier wird für diese Function der Name Massenmatrix gewählt).
Die beiden Functions, mit denen das Differenzialgleichungssystem für den Solver ode45 definiert wird (hier willkürlich Massenmatrix und RechteSeite genannt) empfangen die gleichen Werte: Zeit t und Vektor der Funktionswerte mit φ1(t), φ2(t), ω1(t), ω2(t), so dass gemeinsam mit den gegebenen Parametern der Aufgabenstellung alle Informationen verfügbar sind, um die aktuelle Massenmatrix und die aktuelle rechte Seite des Differenzialgleichungssystems zu berechnen und abzuliefern.
Für Bewegungs-Differenzialgleichungen sind die Standard-Einstellungen in Matlab in der Regel nicht ausreichend. Deshalb sollte immer die "MaxStep"-Option (Voreinstellung: 1) verwendet werden, um die Schrittweite zu verkleinern. Hier wird für eine erste Rechnung der Wert 0.1 eingestellt.
Der in der Datei rk4.m realisierte Runge-Kutta-Algorithmus erwartet nur eine Function, die ihm das Differenzialgleichungssystem beschreibt. Hier wurde dafür die Funtion DopendelDgln eingefügt.
if nargin == 2 % Start mit vorgegebenen Anfangswerten?
x0 = [phi1Anf ; phi2Anf ; 0 ; 0] ; % Anfangswerte [phi1 ; phi2 ; omega1 ; omega2]
else
x0 = [pi/2 ; 0 ; 0 ; 0] ; % Default-Anfangswerte
end
% Parameter (global definiert, damit Wertaenderung nur an einer Stelle erforderlich):
global mdm J1 J2 s1 s2 gdl
mdm = 1 ; J1 = 1./12 ; J2 = 1./12 ; s1 = .5 ; s2 = .5 ; gdl = 9.81 ;
tspan = [0 ; 10] ; % Zeitintervall
% Integration des Anfangswertproblems:
options = odeset('Mass' , @Massenmatrix , 'MaxStep' , 0.1) ;
[t xv] = ode45 (@RechteSeite , tspan , x0 , options) ;
[n nn] = size(t) ; % Anzahl der Zeitschritte
% Runge-Kutta-Algorithmus: --------------------------------------------------
[trk xvrk] = rk4 (@DopendelDgln , tspan , x0 , n) ;
% Grafische Ausgabe von phi1 und phi2, zunaechst "Sortieren der Ergebnisse":
phi1 = xv(:,1) ;
phi2 = xv(:,2) ; % phi1 und phi2 sind Vektoren
phi1rk = xvrk(:,1) ;
phi2rk = xvrk(:,2) ; % phi1i und phi2i sind Vektoren
subplot(3,1,1) ; plot (t , phi1 , 'r' , trk , phi1rk , 'k') , grid on , title ('\phi_1(t)')
subplot(3,1,2) ; plot (t , phi2 , 'r' , trk , phi2rk , 'k') , grid on , title ('\phi_2(t)')
Tq = zeros (n,1) ;
Tqrk = zeros (n,1) ;
om1 = xv(:,3) ;
om2 = xv(:,4) ;
om1rk = xvrk(:,3) ;
om2rk = xvrk(:,4) ;
for i=1:n
Tq(i) = 0.5*(s1^2+J1+mdm)/gdl*om1(i)^2 + 0.5*(mdm*s2^2 + J2)/gdl*om2(i)^2 + (mdm*s2*cos(phi1(i)-phi2(i)))/gdl*om1(i)*om2(i) - (s2+mdm)*cos(phi1(i)) - mdm*s2*cos(phi2(i)) ;
Tqrk(i) = 0.5*(s1^2+J1+mdm)/gdl*om1rk(i)^2 + 0.5*(mdm*s2^2 + J2)/gdl*om2rk(i)^2 + (mdm*s2*cos(phi1rk(i)-phi2rk(i)))/gdl*om1rk(i)*om2rk(i) - (s2+mdm)*cos(phi1rk(i)) - mdm*s2*cos(phi2rk(i)) ;
end
subplot(3,1,3) ; plot (t , Tq , 'r' , t , Tqrk , 'k') , grid on , title ('T_{ges}(t)')
disp(['Ergebnisse nach ' , num2str(length(t)-1) , ' Zeitschritten:']) ; % "End"-Kontrolle
disp(['ode45: phi1 (t_end = ' , num2str(t(end)) , ') = ' , num2str(phi1(end))]) ;
disp(['ode45: phi2 (t_end = ' , num2str(t(end)) , ') = ' , num2str(phi2(end))]) ;
disp(['ode45: |T|_max = ' , num2str(max(abs(Tq))) , ' |T|_min = ' , num2str(min(abs(Tq)))]) ;
disp(['rk4: phi1 (t_end = ' , num2str(t(end)) , ') = ' , num2str(phi1rk(end))]) ;
disp(['rk4: phi2 (t_end = ' , num2str(t(end)) , ') = ' , num2str(phi2rk(end))]) ;
disp(['rk4: |T|_max = ' , num2str(max(abs(Tqrk))) , ' |T|_min = ' , num2str(min(abs(Tqrk)))]) ;
% ============================================================
% Funktion, die die "Massenmatrix" des Dgl.-Systems definiert:
function M = Massenmatrix (t , xv)
global mdm J1 J2 s1 s2 gdl
phi1 = xv(1) ;
phi2 = xv(2) ;
omega1 = xv(3) ;
omega2 = xv(4) ;
c = cos(phi1-phi2);
M = [ 1 0 0 0 ;
0 1 0 0 ;
0 0 s1^2+J1+mdm mdm*s2*c ;
0 0 mdm*s2*c mdm*s2^2+J2 ] ;
% ============================================================
% Funktion, die die "rechte Seite" des Dgl.-Systems definiert:
function xvp = RechteSeite (t , xv) % ... fuer ode45
global mdm J1 J2 s1 s2 gdl
phi1 = xv(1) ;
phi2 = xv(2) ;
omega1 = xv(3) ;
omega2 = xv(4) ;
s = sin(phi1-phi2);
phi1p = omega1 ;
phi2p = omega2 ;
omega1p = -mdm*s2*omega2^2*s - (s1+mdm)*gdl*sin(phi1) ;
omega2p = mdm*s2*omega1^2*s - mdm*s2*gdl*sin(phi2) ;
xvp = [phi1p ; phi2p ; omega1p ; omega2p] ;
% ============================================================
% Funktion, die die Differenzialgleichungen definiert:
function xvp = DopendelDgln (t , xv) % ... fuer rk4
global mdm J1 J2 s1 s2 gdl
phi1 = xv(1) ;
phi2 = xv(2) ;
omega1 = xv(3) ;
omega2 = xv(4) ;
s = sin(phi1-phi2) ;
a11 = s1^2 + J1 + mdm ;
a12 = mdm * s2 * cos(phi1-phi2) ;
a22 = mdm * s2^2 + J2 ;
b1 = -mdm*s2*omega2^2*s - (s1+mdm)*gdl*sin(phi1) ;
b2 = mdm*s2*omega1^2*s - mdm*s2*gdl*sin(phi2) ;
detA = a11 * a22 - a12^2 ;
phi1p = omega1 ;
phi2p = omega2 ;
omega1p = (b1 * a22 - b2 * a12)/detA ;
omega2p = (b2 * a11 - b1 * a12)/detA ;
xvp = [phi1p ; phi2p ; omega1p ; omega2p] ;
- Zu den hellblauen Zeilen: Die Funktion "DoppelPendelKontr" kann aufgerufen werden mit Angabe der Anfangsauslenkungen der beiden Stäbe oder ohne Parameter. Im letztgenannten Fall werden Default-Werte (das sind die Werte der Aufgabenstellung) verwendet.
- Zur weißen Zeile: Mit der Option "Mass" wird angekündigt, dass eine Massenmatrix zu berücksichtigen ist, der folgende Parameter gibt den Namen der dafür bereitgestellten Funktion an. Die Option "MaxStep" ist zwingend, um über ein Zeitintervall von 10 Sekunden ausreichend genaue Ergebnisse zu erzielen (es wird sich herausstellen, dass der zunächst angenommene Wert 0.1 noch nicht für ausreichend kleine Schritte sorgt).
Ergebnisse
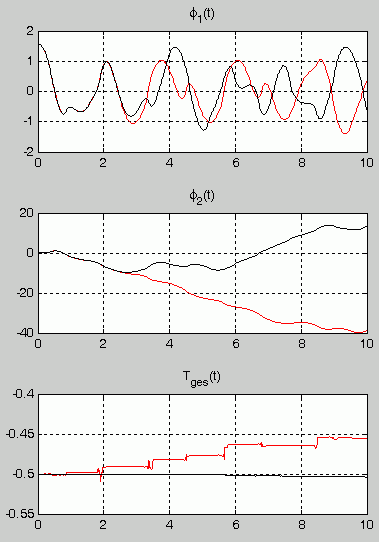
Das Matlab-Script liefert die in der nachstehenden Graphik zu sehenden Bewegungsgesetze φ1(t) und φ2(t). Nach relativ kurzer Zeit gehen die Kurven, die mit den beiden Verfahren berechnet wurden, stark auseinander. Das ist natürlich ein sicheres Indiz dafür, dass mindestens eine der beiden Kurven falsch ist.
Die nachfolgend beschriebenen genaueren Rechnungen zeigen, dass beide falsch sind.
Rechnung mit MaxStep-Parameter 0.1:
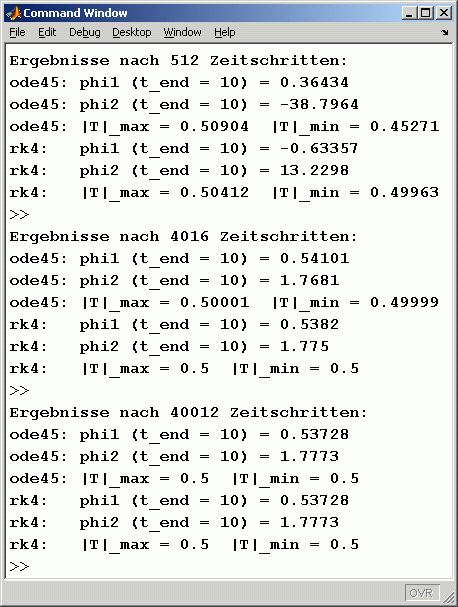
Die Ergebnisse können nur verbessert werden, wenn man über den MaxStep-Parameter feinere Schrittweiten erzwingt. Es wurden drei Rechnungen mit den MaxStep-Werten 0.1, 0.01 und 0.001 durchgeführt. Im Command Window oben rechts sieht man die Protokolle dieser Rechnungen. Es wurden Ergebnisse für 512, 4016 bzw. 40012 Zeitschritte berechnet. Oben links und nachfolgend sieht man die graphischen Darstellungen der Bewegungsgesetze und der Kontrollfunktion.
Die zur Kontrolle ausgegebenen Werte für φ1 und φ2 am Ende des Integrationsintervalls sind ein sehr schönes Indiz dafür, ob mit ausreichend feiner Schrittweite gerechnet wurde. Bei der Rechnung mit der feinsten Schrittweite stimmen alle Werte für beide Verfahren im Rahmen der ausgegebenen Stellen überein, auch die Maxima und Minima der Kontrollfunktion entsprechen in diesem Rahmen genau den Erwartungen.
In der graphischen Darstellung der Kontrollfunktion Tges(t) sieht man allerdings in jedem Fall noch Zacken, was natürlich auf die automatische Maßstabseinstellung zurückzuführen ist. Wenn man zum Beispiel auf der vertikalen Achse einen Bereich von -1 bis +1 einstellt, dann zeigt sich die Kontrollfunktion als horizontale Gerade mit dem konstanten Funktionswert -0.5.
|
Rechnung mit MaxStep-Parameter 0.01: 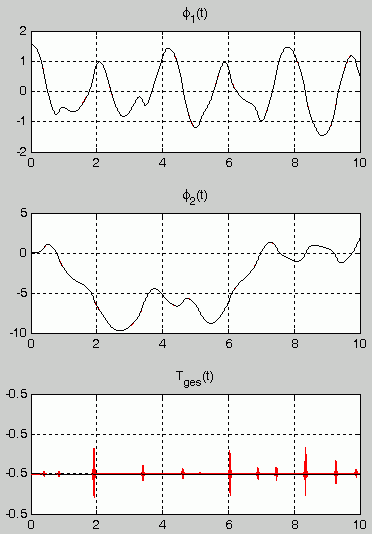
|
Rechnung mit MaxStep-Parameter 0.001: 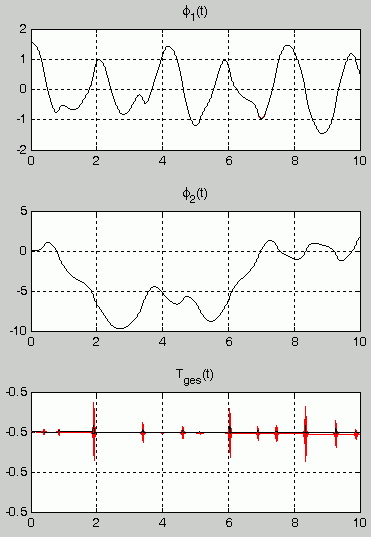
|
