
|
Doppelpendel - Grenzen der Simulation
|
 Achtung, hier wird geschummelt!
Achtung, hier wird geschummelt!
|
|||||
|
Doppelpendel - chaotische Bewegung
Ein Doppelpendel, das nach einmaliger Anregung frei schwingen soll, führt Bewegungen aus, die nur für eine relativ kurze Zeit vorhersagbar sind. Dabei ist die numerische Simulation im Allgemeinen gegenüber dem Experiment im Vorteil, weil die Parameter für die Berechnung exakt bei einer nachfolgenden Rechnung reprodiziert werden können. Am deutlichsten wird das bei den Anfangsbedingungen:
Selbst wenn die Anfangsauslenkungen nur minimal anders sind, ergeben sich nach relativ kurzer Zeit völlig andere Bewegungsabläufe. Das Doppelpendel, das aus diesem Grund ein beliebtes Beispiel in der Chaostheorie ist, eignet sich auch sehr gut für das Ausloten der Grenzen der numerischen Integration von Bewegungs-Differenzialgleichungen.
Aufgabe
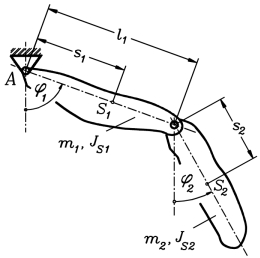
Ein Doppelpendel wird definiert durch die beiden Pendelmassen m1 und m2, die auf die jeweiligen Schwerpunkte bezogenen Massenträgheitsmomente JS1 und JS2, die Schwerpunktabstände von den Drehpunkten s1 und s2 und den Abstand l1 der beiden Drehpunkte voneinander.
Die Aufgabe wird in den Kapiteln "Prinzipien der Mechanik" und "Verifizieren von Computerrechnungen" behandelt.
Die gegebenen Werte gelten für zwei schlanke Stäbe gleicher Masse und gleicher Länge. Sie sollen aus der nebenstehend skizzierten Anfangslage ohne Anfangsgeschwindigkeiten freigelassen werden, so dass folgende Anfangsbedingungen gelten:
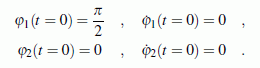
Die Bewegung wird durch die Funktionen φ1(t) und φ2(t) beschrieben. Auf den Seiten "Doppelpendel - Berechnung mit Matlab", "Doppelpendel - Matlab (mit Kontrollen)" und "Doppelpendel - Berechnung mit Simulink" wird gezeigt, welche Einstellungen bei den gewählten Verfahren erforderlich sind, um die Bewegung über einen Zeitbereich t = 0 ... 10 s mit ausreichender Genauigkeit zu simulieren. Hier soll versucht werden, diesen Zeitbereich zu erweitern.
Zunächst aber wird die Abhängigkeit der Bewegung von den Anfansbedingungen demonstriert.
Abhängigkeit der Bewegung von den Anfangsbedingungen
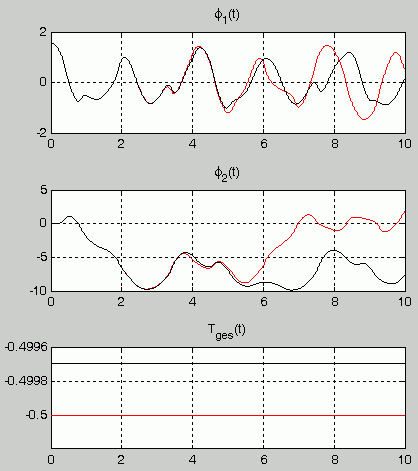
Durch Mehrfachrechnung mit einem Matlab-Script, das zwei verschiedene Integrationsverfahren verwendet, wurden die Einstellungen ermittelt, die praktisch exakte Bewegungsverläufe für das Zeitintervall t = 0 ... 10 s liefern. Die Funktionen, die die beiden Verfahren abliefern, werden in ein Graphikfenster gezeichnet, so dass bei übereinstimmenden Ergebnissen nur eine Kurve zu sehen ist.
Dieses Script wird nun verwendet, um mit einem Verfahren die in der Aufgabenstellung vorgegebene Anfangslage φ1(t=0) = π/2 (mit der bestmöglichen Genauigkeit) zu realisieren, mit dem anderen Verfahren die geringfügig andere Anfangslage φ1(t=0) = 1.571 (π/2 mit vierstelliger Ganauigkeit) vorzugeben (die Abweichung vom exakten Wert ist kleiner als 0,0065%). Das Ergebnis sieht man nebenstehend: Schon nach wenigen Sekunden weichen die Bewegungsverläufe stark voneinander ab und haben am Ende des Integrationsintervalls nichts mehr miteinander zu tun.
Man beachte: Die Abweichungen resultieren nicht aus Verfahrensfehlern. Beide Bewegungsverläufe sind korrekt. Ihre Unterschiede resultieren ausschließlich aus den unterschiedlichen Anfangsauslenkungen.
Berechnung über ein größeres Zeitintervall
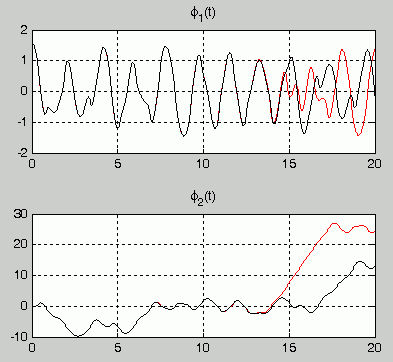
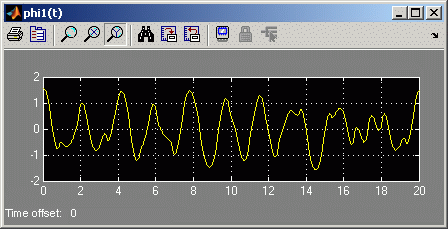
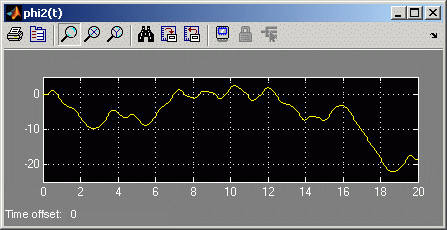
Mit den Einstellungen, mit denen auf den Seiten "Doppelpendel - Matlab (mit Kontrollen)" und "Doppelpendel - Berechnung mit Simulink" erfolgreich über das Zeitintervall t = 0 ... 10 s integriert wurde, soll nun versucht werden, die Lösung für das Zeitintervall t = 0 ... 20 s zu erreichen. Das sind die Ergebnisse:
|
|
|
|
Fazit: Nichts stimmt überein, und die Frage, welche Kurven falsch sind, findet die einfache Antwort: Alle. Es sind zwar mehr als 8000 Zeitschritte berechnet worden, aber das reicht ganz offensichtlich nicht. Man muss die Verfahren zu kleineren Schrittweiten zwingen.
Man beachte: Kein Verfahren gibt einen Hinweis oder eine Warnung aus. Für das Verifizieren der Ergebnisse ist der Berechner allein verantwortlich.
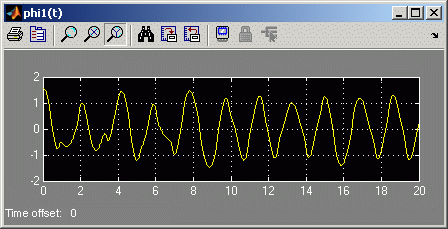
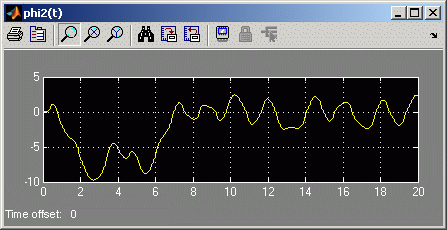
Nachfolgendend sieht man die korrekten Ergebnisse. Der Matlab-Standard-Solver wurde mit der entsprechenden MaxStep-Option gezwungen, Werte für mehr als 80000 Zeitschritte abzuliefern, die Simulink-Rechnung wurde mit den nebenstehend zu sehenden Parametern gesteuert.
Korrekte Ergebnisse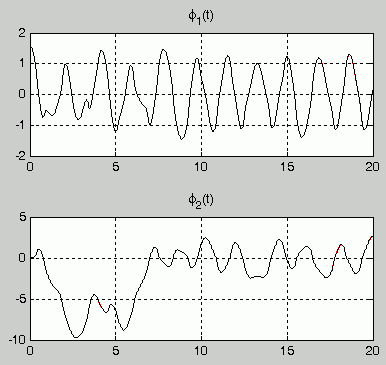
|
|
|
|
Die Grenzen der Berechnungsmöglichkeit, Fazit
Mit den oben gezeigten Ergebnissen für einen Zeitbereich t = 0 ... 20 s sind die Grenzen der Berechnungsmöglichkeit fast erreicht. Trotz drastischer Verkleinerung der Schrittweite lieferte der Versuch, über einen Zeitbereich t = 0 ... 30 s zu rechnen, folgende Ergebnisse:
120 012 Zeitschritte: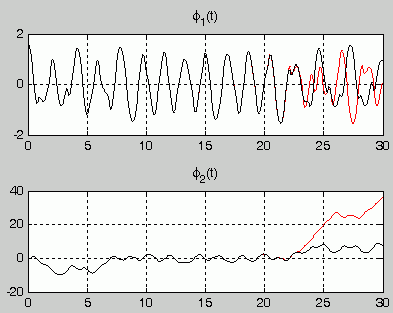
|
1 200 004 Zeitschritte: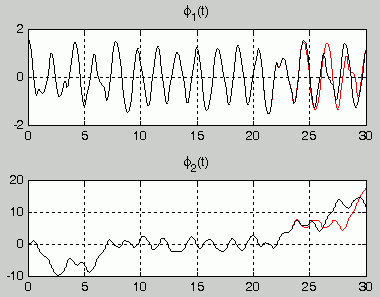
|
Man darf davon ausgehen, dass die Berechnungen nach beiden Verfahren nur bis zu einem bestimmten Punkt richtig sind und dass die voneinander abweichenden Kurven beide falsch sind. Mehr als eine Million Zeitschritte brachten keine befriedigenden Ergebnisse.
Die Simulation der chaotischen Bewegung eines Doppelpendels ist nur über ein sehr eng begrenztes Zeitintervall möglich. Diese Aussage ist nicht den numerischen Lösungsverfahren anzulasten, experimentell hätte man noch viel geringere Chancen.
Es ist auch nicht sinnvoll, über größere Zeitintervalle zu rechnen, denn die unvermeidlichen Fehler in den Parametern und den Anfangsbedingungen haben einen größeren Einfluss auf die Ergebnisse als eventuell auftretende Verfahrensfehler. Auch experimentell dürfte es kaum gelingen, die Anfangsbedingungen zweier Experimente mit der Genauigkeit einzustellen, die identische Bewegungen über einen Zeitraum von 30 Sekunden erzeugen.
Aber für den Test numerischer Verfahren ist das Doppelpendel-Problem gerade deshalb geeignet und sollte als nachdrückliche Erinnerung an die Notwendigkeit des Verfizierens von Computerrechnungen im Gedächtnis bleiben.
Natürlich ist auch die Animation der chaotischen Bewegung reizvoll. Nachfolgend sieht man links die Bewegung entsprechend der Aufgabenstellung für einen Zeitbereich von 10 Sekunden. Danach wird die Animation angehalten und neu gestartet.
Rechts wird geschummelt. Es wurde eine Anfangsauslenkung gefunden, die nach einer gewissen Zeit ganz ähnlich als momentane Lage der beiden Pendel wieder erscheint. In diesem Fall sind es etwa 8 Sekunden, die korrekt wiedergegeben und anschließend immer wiederholt werden. Das hat natürlich nichts mit der sich tatsächlich ergebenden Bewegung zu tun (sieht aber lustig aus).
Der Animation über 10 Sekunden darf man in diesem Fall vertrauen: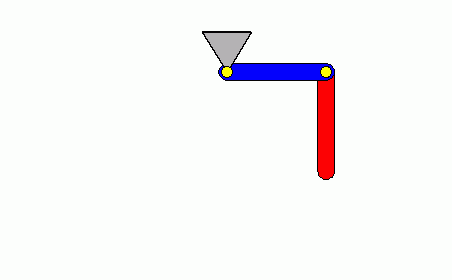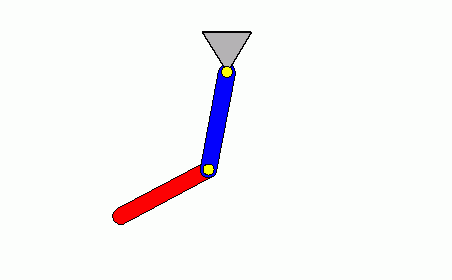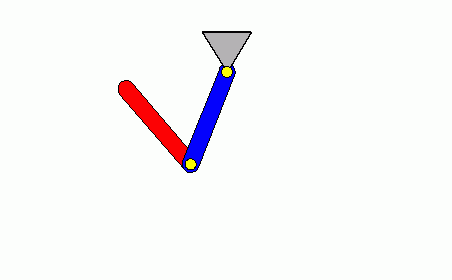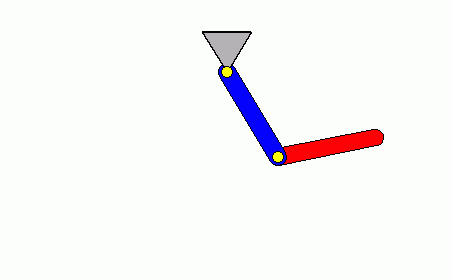
|
Ein "Dauerläufer" ist in jedem Fall geschummelt. Hier
wird ein "Animated GIF" immer wieder abgespielt:
|
Man findet im Internet eine ganze Reihe von Doppelpendel-Animationen, die fast alle den Eindruck erwecken, als würde die Bewegung tatsächlich berechnet. Möglicherweise wird sogar gerechnet. Es ist bei diesen Anfangswertproblemen wie bei den komfortablen Programmen der Finite-Elemente-Methode: Die Computer-Graphik stellt klaglos jeden beliebigen Unsinn mit schönen bunten Bildern dar.
